Предмет: Математика,
автор: NikitaKonoplev
Решить интеграл (Интегральное исчисление функции одной переменной)
Приложения:
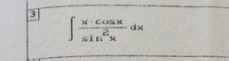
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: hegoxi9306
Предмет: Математика,
автор: 22068526
Предмет: Литература,
автор: lolkek88251
Предмет: Математика,
автор: zirina1970
Предмет: Алгебра,
автор: Аноним