Question

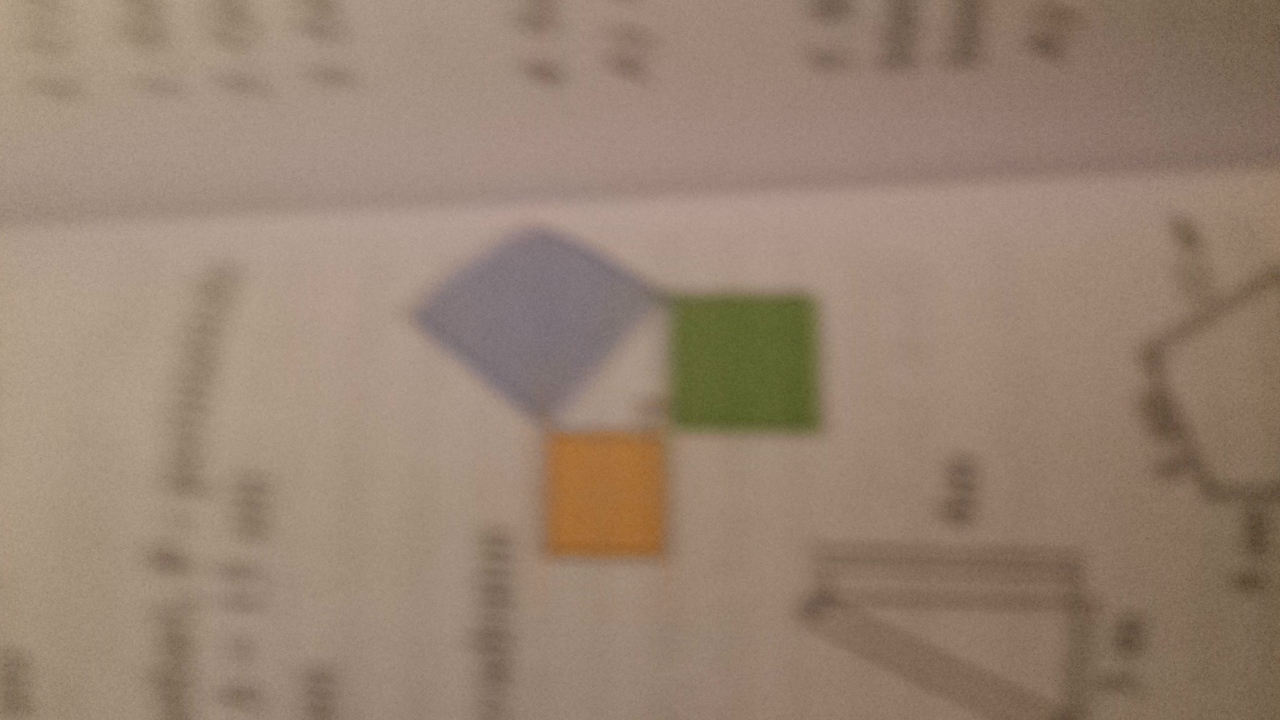
На рисунке , три квадрата. Их общая площадь 200 м^2. найдите площадь большего квадрата

Answer 1

а - сторона жёлтого квадрата,  а² - его площадь.
b - сторона зелёного квадрата, b² - его площадь
с - сторона синего квадрата, с² - его площадь. 
С другой стороны а, b, с - это стороны прямоугольного треугольника, лежащего между данными квадратами.
а, b - катеты
с - гипотенуза
По теореме Пифагора 
а² + b² = с²
По условию а² + b² + с² = 200м²
Заменив сумму  (а² + b²) квадратом с², получим
с² + с² = 200
2с² = 200
с² = 200 : 2
с² = 100
Ответ: 100 м²

Answer 2

Спасибо дружище

Answer 3

Ок!