Предмет: Алгебра,
автор: Ametorry
Высшая математика. Прошу, помогите :).
Приложения:
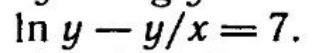
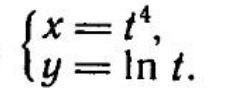
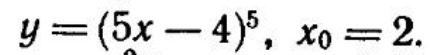
Ответы
Автор ответа:
0
1) Производная неявной функции:


2) производная функции заданной параметрически:

3) Производная сложной функции:

2) производная функции заданной параметрически:
3) Производная сложной функции:
Автор ответа:
0
спасибо большое :)
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Физика,
автор: Demanaize
Предмет: Биология,
автор: ga234662p7ua4f
Предмет: Литература,
автор: hairutdinova200
Предмет: Математика,
автор: suny10