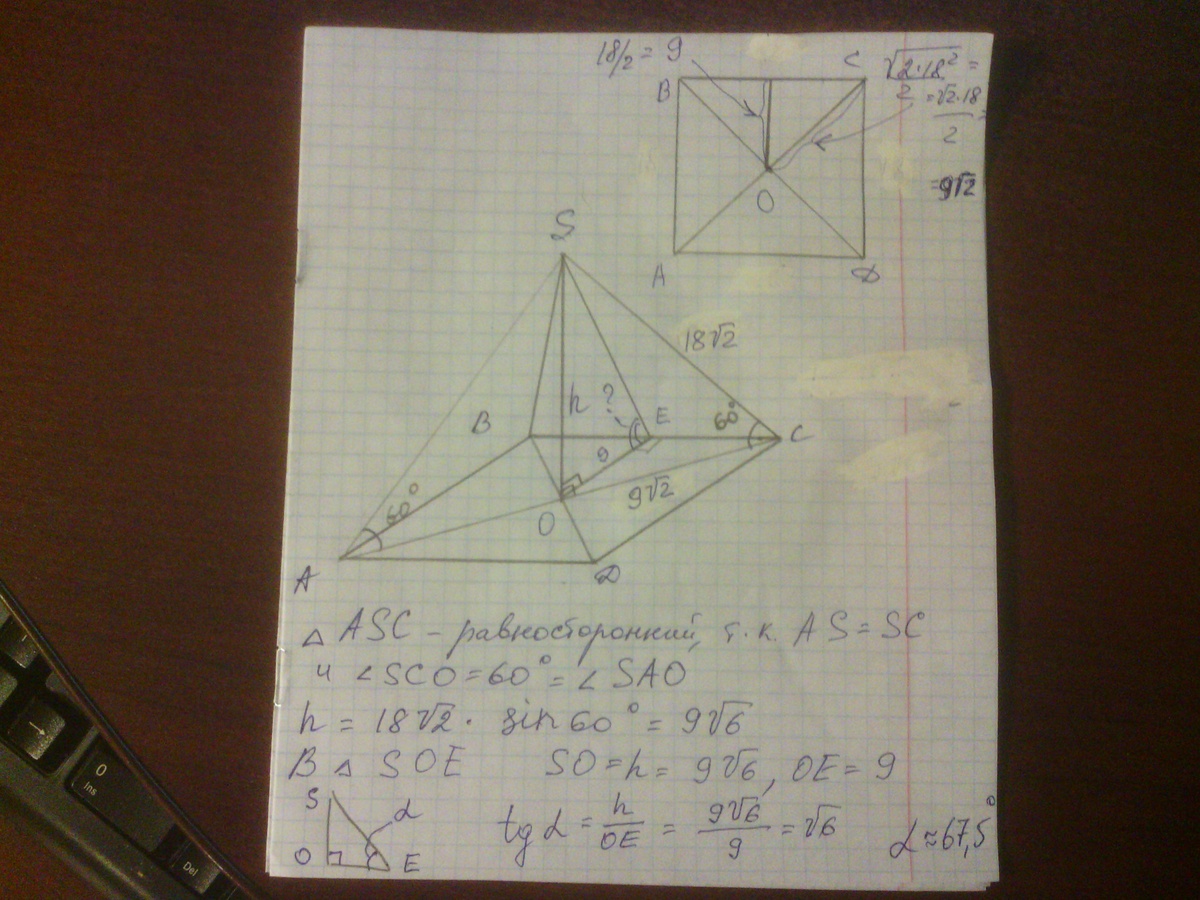
Через центр О квадрата ABCD проведен к его плоскости перпендикуляр SO. Угол между прямой SC и плоскостью квадрата равна 60 °, АВ = 18 см. Найдите угол между плоскостями ABC и BSC.
Ответы
Данный двугранный угол равен линейному SEO, где Е - середина стороны AD.
Квадрат со стороной 18 имеет диагональ 18 корней из 2, половина этой диагонали - отрезок ОА - равен 9 корней из 2. Из треугольника ASO находим:
SA = 18 корней из 2.
Поскольку в основании квадрат, то SA = SD, треугольник ASD равнобедренный с тремя известными нам сторонами: 18 корней из 2; 18 корней из 2; 18.
Высота, проведенная к основанию SE = 9 корней из 7.
Отрезок ОЕ = 18/2 = 9
Косинус угла SEO равен (корень из 7)/7
Искомый угол равен arccos√7/7.
см вложение......................................................