Предмет: Алгебра,
автор: f2f4f6
Помогите решить системы уравнений
Приложения:
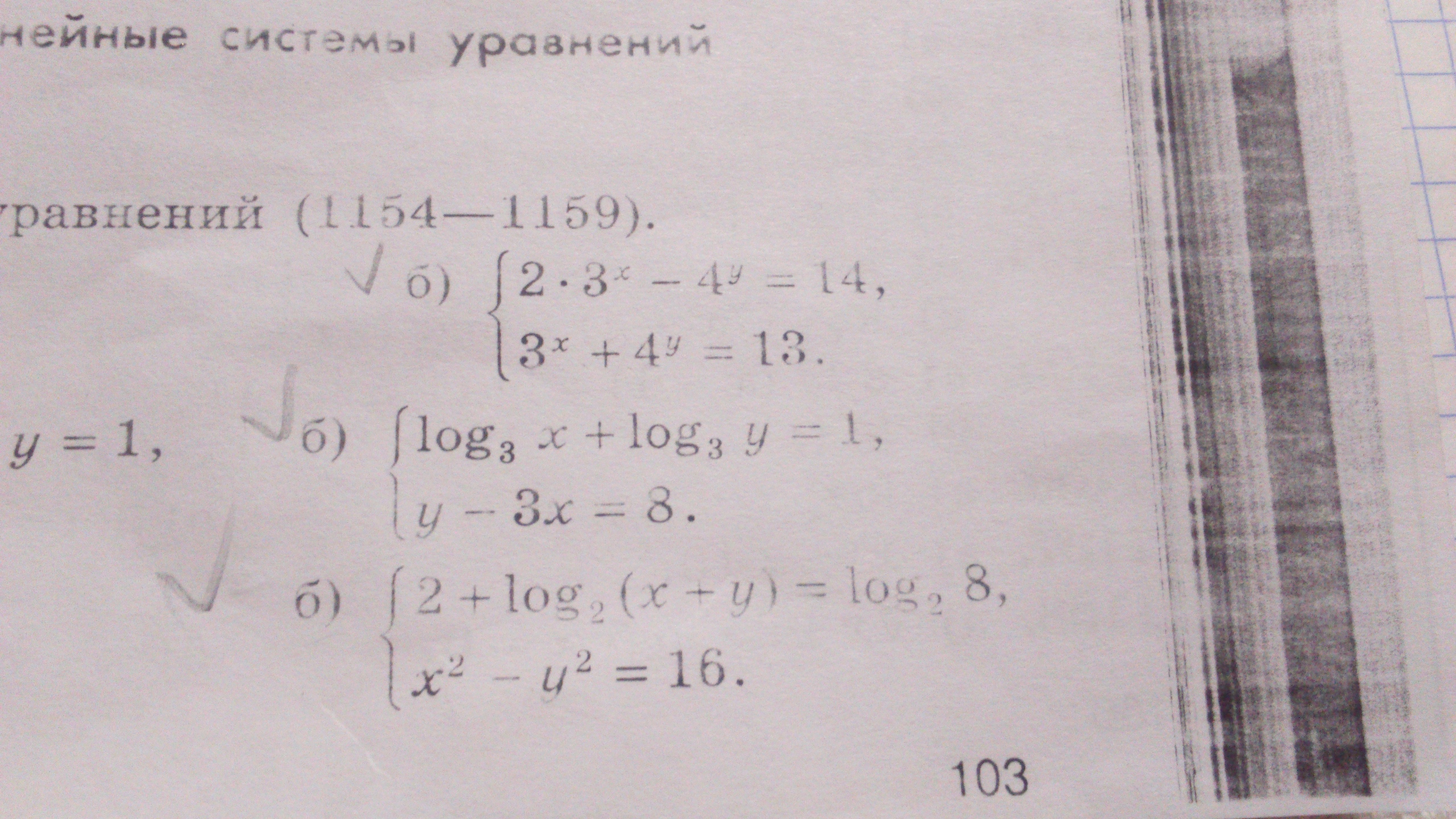
Ответы
Автор ответа:
0
1)

x=2, y=1
2)

x=1/3, y=9. Мы выкинули отрицательный корень x, потому что нельзя брать логарифмы отрицательных чисел
3)

x = 5 y= -3
x=2, y=1
2)
x=1/3, y=9. Мы выкинули отрицательный корень x, потому что нельзя брать логарифмы отрицательных чисел
3)
x = 5 y= -3
Похожие вопросы
Предмет: Русский язык,
автор: gulievaadelia
Предмет: Русский язык,
автор: milashka8575
Предмет: Биология,
автор: kiselevaaleksandra66
Предмет: Информатика,
автор: anyapolukhina
Предмет: Математика,
автор: liberty0305