Предмет: Алгебра,
автор: motkinmaks
Решить предел по правилу Лопиталя.

Добавил фото, на всякий случай.
Приложения:
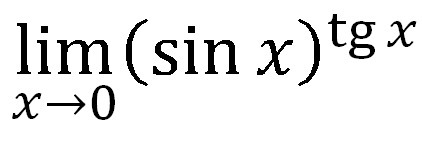
Ответы
Автор ответа:
0
Вычислим отдельно
limtgx*ln(sinx)=lim[ln(sinx)/(ctgx)]=lim[(ln(sinx)]`/(ctgx)`=
=lim[1/sinx*cosx^(-1/cos²x]=lim(-cosx/sinx *sin²x)=lim(-sinx*cosx)=lim(-1/2*sin2x)=-1/2*0=0
Нашли степень e
Таким образом
Похожие вопросы
Предмет: Английский язык,
автор: mayamu68
Предмет: Английский язык,
автор: svetafinchenko
Предмет: Математика,
автор: anzhelakudenko
Предмет: Физика,
автор: dariyaguk
Предмет: Биология,
автор: alex888508