Question

ПОМОГИТЕ ПОЖАЛУЙСТА!!!
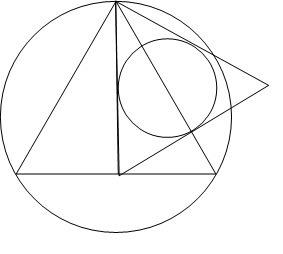
В окружность,диаметр которой равен корень 12,вписан правильный треугольник. На его высоте как на стороне построен другой правильный треугольник,в который вписана окружность.
Найти радиус этой новой окружности.

Answer 1

d=√12=2√3, R=2√3/2=√3
Сторона правильного треугольника вписанного в окружность равна
a=R√3=√3*√3=3.
Высота правильного треугольника можно вычислить по формуле
h=a√3/2=3√3/2.
Высота треугольника равна стороне нового правильного треугольника
a2=h=3√3/2.
Радиус вписанной окружности можно вычислить по формуле
r=a2√3/6=3√3/2*√3/6=9/2*1/6=3/4=0,75
Ответ: 0,75.