Question

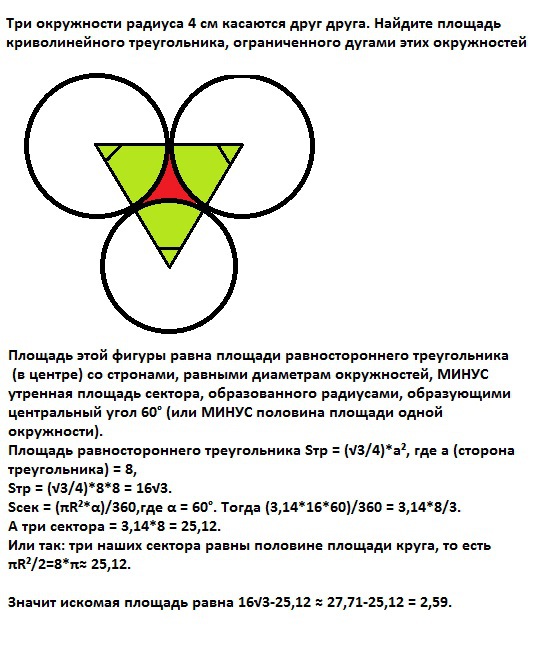
три окружности радиуса 4 см касаются друг друга. Найдите площадь криволинейного треугольника, ограниченного дугами этих окружностей

Answer 1

Площадь этой фигуры равна площади равностороннего треугольника  (в центре) со сторонами, равными диаметрам окружностей, МИНУС утроенная площадь сектора, образованного радиусами, образующими центральный угол 60° (или МИНУС половина площади одной окружности).
Площадь равностороннего треугольника Sтр = (√3/4)*а²,
(где а - сторона треугольника = 8),
Sтр = (√3/4)*8*8 = 16√3.
Sсек = (πR²*α)/360,где α = 60°. Тогда (π*16*60)/360 = π*8/3.
А три сектора = π*8 ≈ 25,12.
Или так: три наших сектора равны половине площади круга, то есть πR²/2=8*π≈ 25,12.
 
Значит искомая площадь равна 16√3-25,12 ≈ 27,71-25,12 = 2,59.