Question

Докажите, что биссектрисы вертикальных углов лежат на одной прямой

Answer 1

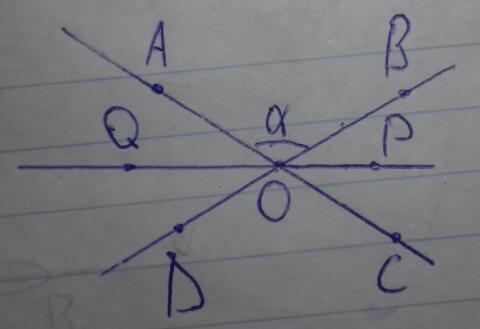
AC ∩ BD = O

Пусть ∠AOB=α, тогда ∠BOC=180°-α т.к. ∠AOB и ∠BOC смежные; так же ∠AOD=180° - α.

OP - биссектриса ∠BOC; OQ - биссектриса ∠AOD; ∠BOC и ∠AOD вертикальные.

∠BOP = ∠BOC÷2 = $tt dfrac{180^{circ } -alpha }2$ т.к. биссектриса делит угол пополам; так же ∠AOQ = ∠AOD÷2 = $tt dfrac{180^{circ } -alpha }2$

∠QOP = ∠AOQ+∠AOB+∠BOP = $tt dfrac{180^{circ } -alpha }2 +alpha +dfrac{180^{circ } -alpha }2 =alpha +180^{circ } -alpha =180^{circ }$

Значит ∠QOP развёрнутый ⇒ OQ,OP ⊂ QP. Доказано.