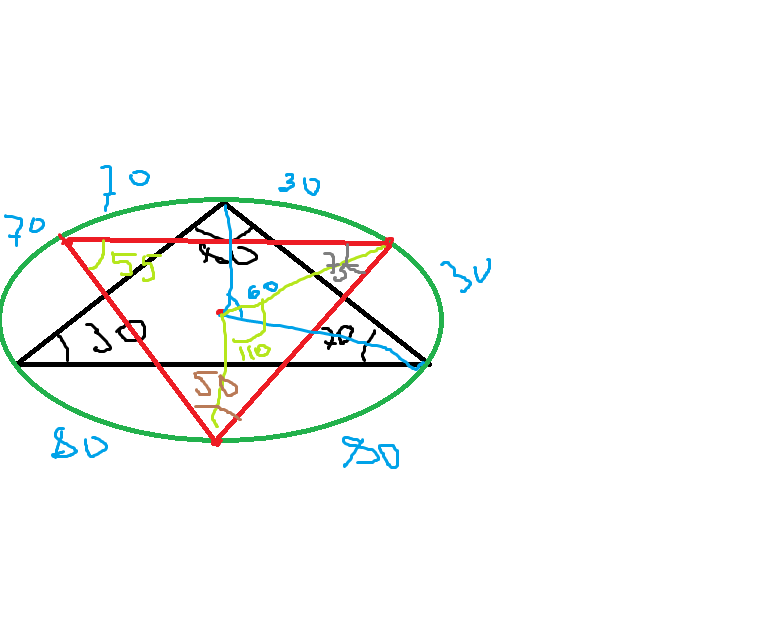
Около треугольника с углами 30,70,80, описана окружность.Определите углы треугольника ,вершины которого совпадают с серединами меньших дуг,стягиваемых сторонами данного треугольника.
Ответы
Интересное задание, давно не встречал.
Итак, пусть это будет ΔАВС, угол А=80⁰, угол В=30⁰, угол С=70⁰
Все углы А, В и С - вписанные углы, опирающиеся на меньшие дуги ВС, АС и АВ, соответственно. Поскольку вписанный угол равен половине градусной величины дуги, на которую он опирается, то:
Дуга ВС=160⁰
Дуга АС=60⁰
Дуга АВ=140⁰
Точки М, N, К - середины дуг ВС, АС и АВ, соответственно, и делят дуги ВС, АС и АВ пополам. Таким образом:
Дуга ВМ=дуге МС=80⁰
Дуга CN=дуге NA=30⁰
Дуга АК=дуге КВ=70⁰
Углы М, N, К - также вписанные углы, опирающиеся на дуги KN, KM и MN, соответственно, которые равны:
Дуга КN=дуга NA+дуга АК=30⁰+70⁰=100⁰
Дуга КМ=дуга КВ+дуга ВМ=70⁰+80⁰=150⁰
Дуга MN=дуга МС+дуга CN=80⁰+30⁰=110⁰
Углы M, N и К равны половинам градусных величин дуг KN, KM и MN, соответственно:
Угол М=50⁰
Угол N=75⁰
Угол К=55⁰
Как "Лучшее решение" не забудь отметить, ОК?!.. ;)))
Делим окружность на соответствующие дуги и пользуясь свойством вписанный угол равен половине сответствующего центрального(опирающегося на одну и ту же дугу) получаем
55, 75,50
см вложение