Постройте график функции (в приложении) и определите, при каких значениях параметра с прямая y=c не имеет с графиком функции общих точек. Буду благодарна и просто за упрощение функции
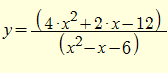
Ответы
Упрощение числителя:
4x^2 + 2x - 12 = 4(x-6/4)(x+2) = (4x-6)(x+2)
D = 4 - 4*4*(-12) = 196 = 14^2
x1 = -2 +14/8 = 12/8 = 6/4
x2 = -2-14/8 = -16/8 = -2
Упрощение знаменателя:
x^2-x-6 = (x-3)(x+2)
D = 1-4*1*(-6) = 25
x1 = 1+5/2 = 3
x2 = 1-5/2 = -2
Получается функция:
y = (4x-6)(x+2)/(x-3)(x+2) = 4x-6/x-3
y = 4x-6/x-3
то есть надо найти асимптоту функций то есть ее предел при х стремящиймся к бесконечности
y=lim x--- > oo(4x^2+2x-12)/(x^2-x-6)
тогда поделим числитель и знаменатель на x^2
получим
y=4+2/x-12/x^2/ 1-1/x-6/x^2
2/x стреимться к 0 и остальные так же
ответ y=4 значит с равен 4