Нужна помощь. Помогите решить эти задания, ну или хотя бы подскажите с чего начать решать данные неравенства?
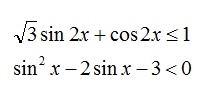
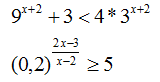
Ответы
в 1) применить формулы двойного аргумента: sin2x = 2sinx*cosx cos2x = 1-2(sinx)^2
потом общий множитель sinx вынести за скобку... и неравенство сведется к двум:
sinx <= 0 и второе, кот. сводится к неравенству относительно tgx...
2) квадратное относительно sinx ---просто ввести новую переменную...
3) 9^(x+2) + 3 < 4*3^(x+2) ---тоже квадратное относительно 3^(x+2) === t
t^2 + 3 - 4t < 0
4) 0.2 =2/10 = 1/5 = 5^(-1)
5^( (3-2x) / (x-2) ) >= 5^1
(3-2x) / (x-2) >= 1
..............................................
Можно пойти двумя путями - через подстановку тангенс икс, либо разделив все на 2 и заметив, что имеем дело с формулой "синус суммы":
Второе - происто квадратичное неравенство относительно синуса. (sinx-3)(sinx+1)<0
Понятно, что первая скобка всегда <0, а вторая >=0. Итого, нам просто не подходят все точки, в кoторых sinx=-1, т.е. x!=-pi/2+2pi*n
Третье - то же самое, что и во втором, замена t=3^(x+1) приводит к неравенству t^2-4t+3<0, откуда t in (1,3). Поэтому x+1 in (0,1), а x in (-1,0).
Четвертое - стандартное неравенство 0.2^(...)>=0.2^(-1)
(2x-3)/(x-2)<=-1
(2x-4+3)/(x-2)<=-1
2+3/(x-2)<=-1
3/(x-2)<=-3
1/(x-2)<=-1
-1<=x-2<0
1<=x<2