Предмет: Математика,
автор: aceaxe
Вычислить площадь фигуры, ограниченной указанными линиями.+ чертеж
Приложения:
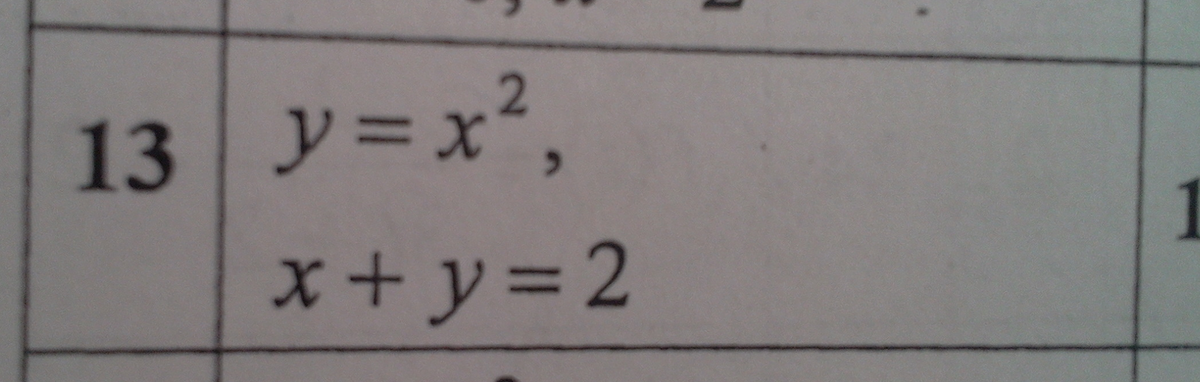
Ответы
Автор ответа:
0
Сначала ищем точки пересечения графиков:
f(x) = x^2
g(x) = 2-x
f(x) = g(x)
x^2 = 2-x
x^2 + x - 2 = 0
x1 = -2
x2 = 1
Площадь фигуры ограниченной графиками равна
В нашем случае получаем:
Похожие вопросы
Предмет: Экономика,
автор: Аноним
Предмет: Другие предметы,
автор: lubakusenko979
Предмет: Литература,
автор: sakhipovamalikusha1
Предмет: Химия,
автор: lenchik96