Предмет: Математика,
автор: Аноним
1. Вычислите площадь фигуры, ограниченной линиями у=х^2 и у =2х
2.Найдите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченного линиями у^2=х и у=х^2
Ответы
Автор ответа:
0
Дано
y1=x², y2 = 2x.
Сначала находим пределы интегрирования решением системы уравнений.
x² - 2x = 0 = х*(х-2)
Корни - х1 = 0 и х2 = 2.
Прямая у=2х - выше параболы, поэтому площадь вычисляется по формуле

ОТВЕТ S=4/3.
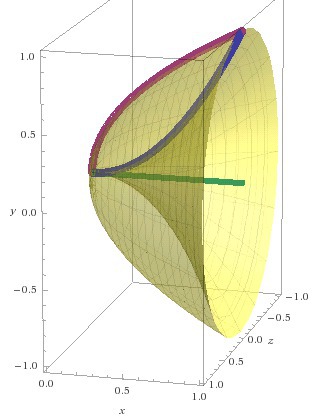
2. Объем фигуры по формулам
Формулы для вычисления объема фигуры.
y₁=x² y₂²=x - пределы интегрирования от 0 до 1.

В результате объем равен разности
V=V1-V2 =3/10*π ~0.94 - ОТВЕТ
y1=x², y2 = 2x.
Сначала находим пределы интегрирования решением системы уравнений.
x² - 2x = 0 = х*(х-2)
Корни - х1 = 0 и х2 = 2.
Прямая у=2х - выше параболы, поэтому площадь вычисляется по формуле
ОТВЕТ S=4/3.
2. Объем фигуры по формулам
Формулы для вычисления объема фигуры.
y₁=x² y₂²=x - пределы интегрирования от 0 до 1.
В результате объем равен разности
V=V1-V2 =3/10*π ~0.94 - ОТВЕТ
Приложения:
Похожие вопросы
Предмет: Физика,
автор: kcistakov100
Предмет: Обществознание,
автор: jay888
Предмет: История,
автор: vladislav51pavuc
Предмет: Физика,
автор: dumanbik
Предмет: Физика,
автор: marinagolubiev