Question

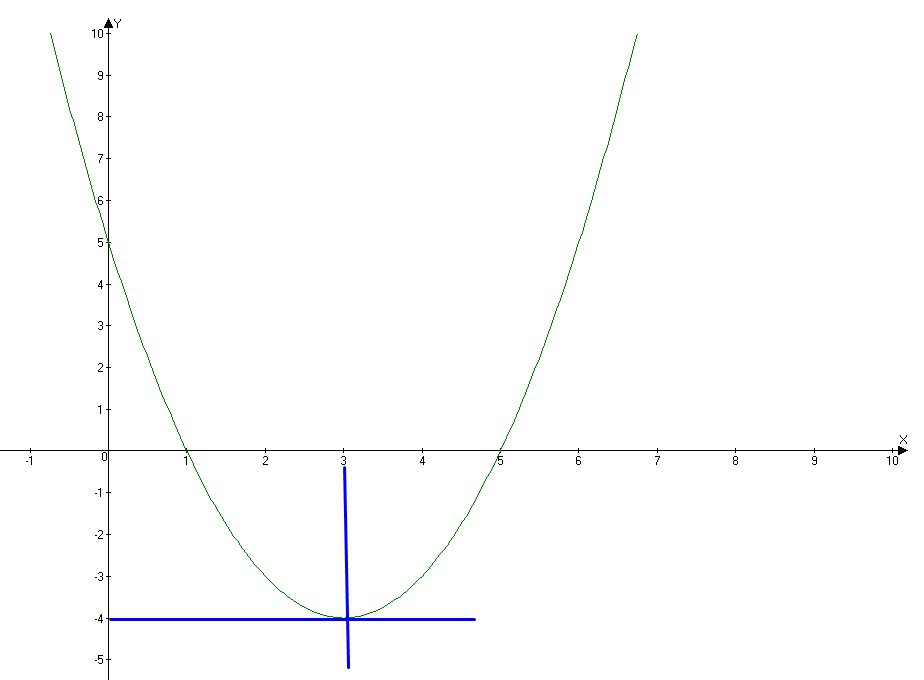
Постройте график функции y=x^2 - 6x + 5. Найдите с помощью графика:
а)значение y при x=0.5
б)значения x при которых y=-1
в)нули функции; промежутки, в которых y>0 и в которых y<0
г)промежуток на котором функция возрастает.

Answer 1

Найдем вершину параболы

$x=- frac{b}{2a} =- frac{-6}{2} =3$

$y=3^2-6cdot3+5=-4$

(3;-4) - координаты вершины параболы.

а) Найдем значение у при х=0,5

$y(0.5)=(0.5)^2-6*0.5+5=2.25$

б) Значения х при у=-1
$-1=x^2-6x+5\ x^2-6x+6=0\ D=b^2-4ac=36-24=12\ \ x_1_,_2= dfrac{-bpm sqrt{D} }{2a} = dfrac{6pm2 sqrt{3} }{2} =3pm sqrt{3}$

в) Нули функции, промежутки, в которых y>0 и y<0
$x^2-6x+5=0$
По т. Виета: $x_1=5;,,,,,x_2=1$ - нули функции
$y textgreater 0$, т.е. $x^2-6x+5 textgreater 0$
По графику $y textgreater 0$ это будет промежутки $x textless 1;,,,x textgreater 5$, а $y textless 0$, т.е. $x^2-6x+5 textless 0$ это будет промежуток $1 textless x textless 5$

г) Промежуток в котором функция возрастает - $x in (3;+infty)$