Предмет: Алгебра,
автор: Алинка0707
Помогите решить 3 примера!
Во вложении!
Пожалуйста, нужно с графиком...
C 1- 3
Все свои баллы даю....
Приложения:
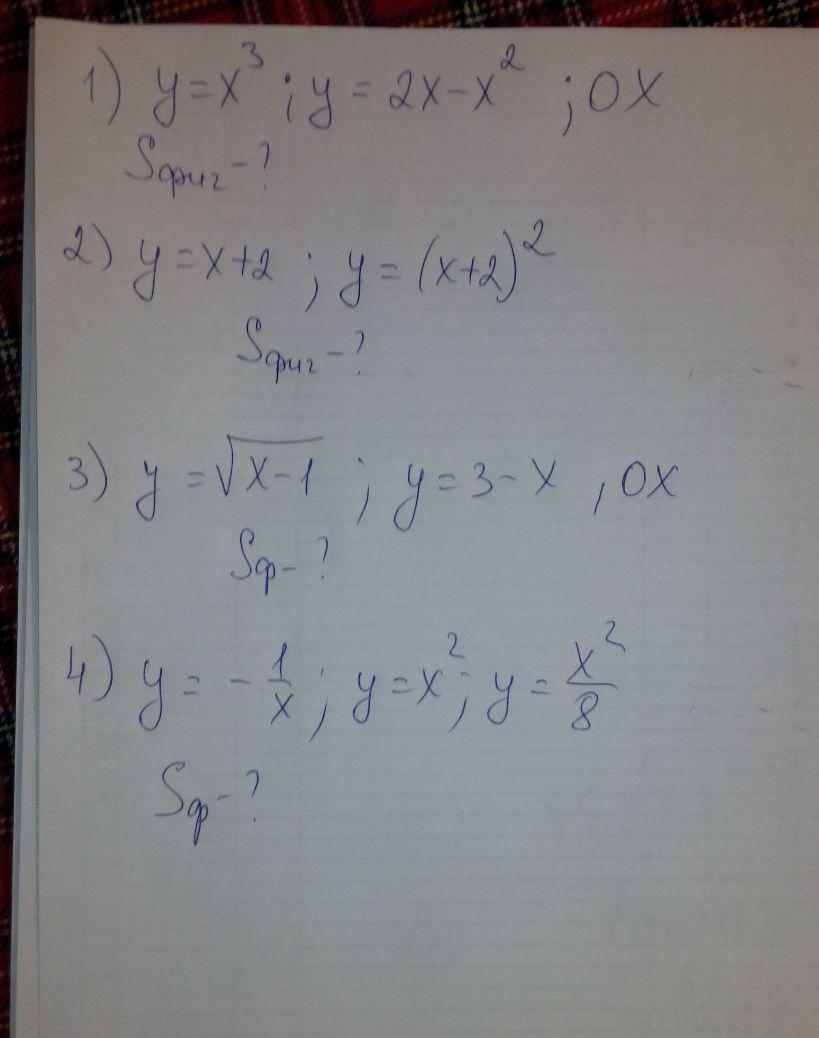
Ответы
Автор ответа:
0
1
y=x³ кубическая парабола
х -2 -1 0 1 2
у -8 -1 0 1 8
у=-х²+2х=-(х-1)²+1 парабола у=-х²,с вершиной в точке(1;1),точки пересечения с осями (0;0) и (2;0)
Получили фигуру ограниченную сверху параболой у=-х²+2х,а снизу параболой у=х³.Точки пересечения (0;0) и (1;1).
 =(-x³/3+x²-x^4/4)|1-0=
=(-x³/3+x²-x^4/4)|1-0=
=-1/3+1-1/4=1-7/12=5/12ед²
2
у=х+2 прямая
х -2 0
у 0 2
у=(х+2)² парабола у=х² с вершиной в точке (-2;0).
Фигура ограничена сверху прямой,а снизу параболой.
Точки пересечения (-2;0) и (-1;1)
Площадь равна интегралу от функции (х+2-(х+2)²)=х+2-х²-4х-4)=
=-х²-х-2 в пределах от -2 до -1.
S=-x³/3-x²/2-2x|-1-(-2)=1/3-1/2+2+8/3+2-4=2,5ед²
3
y=√(x-1) ветвь параболы
х 1 5 10
у 0 2 3
у=3-х прямая
х 0 3
у 3 0
Точка пересечения (2;1)

 2/3*√(x-1)³|2-1 +(3x-x²/2)|3-2=2/3*1-2/3*0+9-9/2-6+2=
2/3*√(x-1)³|2-1 +(3x-x²/2)|3-2=2/3*1-2/3*0+9-9/2-6+2=
=2/3+1/2=7/6=1 1/6ед²
y=x³ кубическая парабола
х -2 -1 0 1 2
у -8 -1 0 1 8
у=-х²+2х=-(х-1)²+1 парабола у=-х²,с вершиной в точке(1;1),точки пересечения с осями (0;0) и (2;0)
Получили фигуру ограниченную сверху параболой у=-х²+2х,а снизу параболой у=х³.Точки пересечения (0;0) и (1;1).
=-1/3+1-1/4=1-7/12=5/12ед²
2
у=х+2 прямая
х -2 0
у 0 2
у=(х+2)² парабола у=х² с вершиной в точке (-2;0).
Фигура ограничена сверху прямой,а снизу параболой.
Точки пересечения (-2;0) и (-1;1)
Площадь равна интегралу от функции (х+2-(х+2)²)=х+2-х²-4х-4)=
=-х²-х-2 в пределах от -2 до -1.
S=-x³/3-x²/2-2x|-1-(-2)=1/3-1/2+2+8/3+2-4=2,5ед²
3
y=√(x-1) ветвь параболы
х 1 5 10
у 0 2 3
у=3-х прямая
х 0 3
у 3 0
Точка пересечения (2;1)
=2/3+1/2=7/6=1 1/6ед²
Приложения:
Автор ответа:
0
Огромное спасибо!)
Автор ответа:
0
Как будет доступна кнопка лучшее, поставлю сразу же)
Похожие вопросы
Предмет: Математика,
автор: abdukoshadqq
Предмет: География,
автор: ramazanabduhalikov61
Предмет: Алгебра,
автор: kratijruslan
Предмет: Математика,
автор: 198605az30