Предмет: Алгебра,
автор: Аноним
срочно пожалуйста заранее спасибо
Приложения:
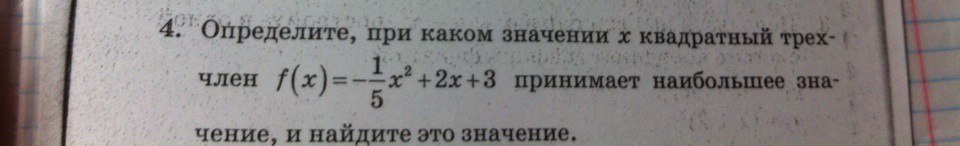
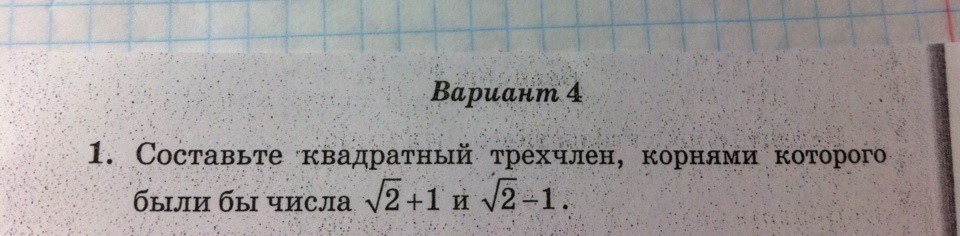
Ответы
Автор ответа:
0
№1
По теореме Виета, для квадратного уравнения x²+bx+c справедливы такие соотношения:
x1+x2=-b,
x1*x2=c.
Известно, что x1=√2+1, x2=√2-1
Тогда x1+x2=√2+1+√2-1=2√2=-b, b=-2√2
x1*x2=(√2+1)(√2-1)=(√2)²-1²=1=c
Искомый квадратный трехчлен:
x²-2√2x+1
№4
Наибольшее значение квадратный трехчлен принимает в своей вершине, так как это парабола с ветвями вниз. Координата x вершины определяется как -b/(2a), где b=2, a=-1/5. xв=-2/(2*(-1/5))=5.
Координата y вершины определяется как значение функции f(x) в координате x вершины. То есть yв=f(xв)=-1/5*5²+2*5+3=8
Таким образом, квадратный трехчлен f(x) принимает наибольшее значение при x=5. Оно равно f(5)=8.
По теореме Виета, для квадратного уравнения x²+bx+c справедливы такие соотношения:
x1+x2=-b,
x1*x2=c.
Известно, что x1=√2+1, x2=√2-1
Тогда x1+x2=√2+1+√2-1=2√2=-b, b=-2√2
x1*x2=(√2+1)(√2-1)=(√2)²-1²=1=c
Искомый квадратный трехчлен:
x²-2√2x+1
№4
Наибольшее значение квадратный трехчлен принимает в своей вершине, так как это парабола с ветвями вниз. Координата x вершины определяется как -b/(2a), где b=2, a=-1/5. xв=-2/(2*(-1/5))=5.
Координата y вершины определяется как значение функции f(x) в координате x вершины. То есть yв=f(xв)=-1/5*5²+2*5+3=8
Таким образом, квадратный трехчлен f(x) принимает наибольшее значение при x=5. Оно равно f(5)=8.
Похожие вопросы
Предмет: Окружающий мир,
автор: kovalenkoelizaveta73
Предмет: Геометрия,
автор: liliyatolmaceva
Предмет: Химия,
автор: htssp
Предмет: Геометрия,
автор: aruka201