1) Одно из оснований трапеции равно 15, высота 10, а площадь 200. Найдите второе основание трапеции.
2) Высота трапеции равна 10, а площадь равна 210. Найдите среднюю линию трапеции.
3)Основания равнобедренной трапеции равны 5 и 29, а ее периметр равен 74. Найдите площадь трапеции.
Ответы
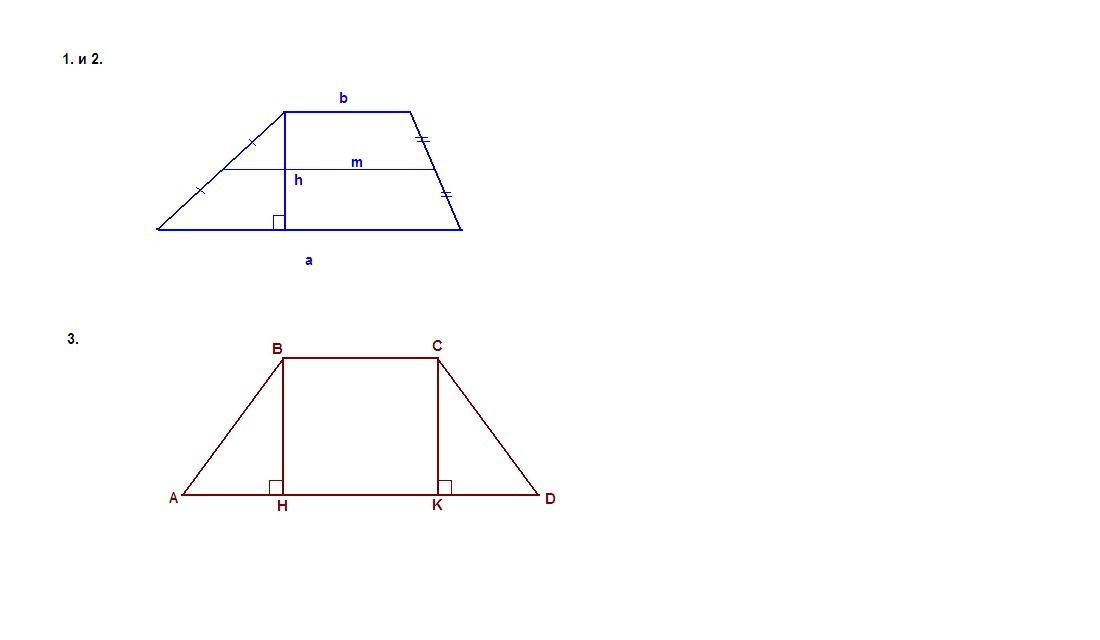
Обозначим основания трапеции а и b, h - высота трапеции, S - ее площадь, m - средняя линия трапеции.
1) a = 15, h = 10, S = 200
S = (a + b)/2 · h
200 = (15 + b)/2 · 10
(15 + b)/2 = 200 / 10
(15 + b)/2 = 20
15 + b = 20 · 2
15 + b = 40
b = 40 - 15
b = 25
2) h = 10, S = 210.
Средняя линия трапеции равна полусумме оснований:
m = (a + b)/2
S = (a + b)/2 · h = m · h
m = S / h
m = 210 / 10
m = 21
3) Pabcd = AD + BC + 2AB
2AB = Pabcd - (AD + BC)
2AB = 74 - (5 + 29) = 40
AB = CD = 40/2 = 20
Проведем ВН и СК - высоты. Они равны и параллельны, значит ВНКС - прямоугольник, НК = ВС = 5.
ΔАВН = ΔDCK по катету и гипотенузе (ВН = СК, АВ = CD), ⇒
АН = KD = (AD - BC)/2 = (29 - 5)/2 = 12
Из прямоугольного треугольника АВН по теореме Пифагора:
ВН = √(AB² - AH²) = √(20² - 12²) = √(400 - 144) = √256 = 16
S = (AB + BC)/2 · BH
S = (29 + 5)/2 · 16 = 34/2 · 16 = 17 · 16 = 272