Предмет: Алгебра,
автор: ЕнотЕнотыч
Найдите наибольшее и наименьшее значение функции на промежутке [1;6].
на промежутке [1;6].
Не знаю как быть: приятель говорит, что производные они не брали, т.к. исключили из программы. Можно ли решить это задание без производных?
Ответы
Автор ответа:
0
Используем свойства функций.Т.к. Х³-3Х-возр.,то 1/Х³-3Х-убывающая.Считаем значения функции на концах отрезка.
Приложения:
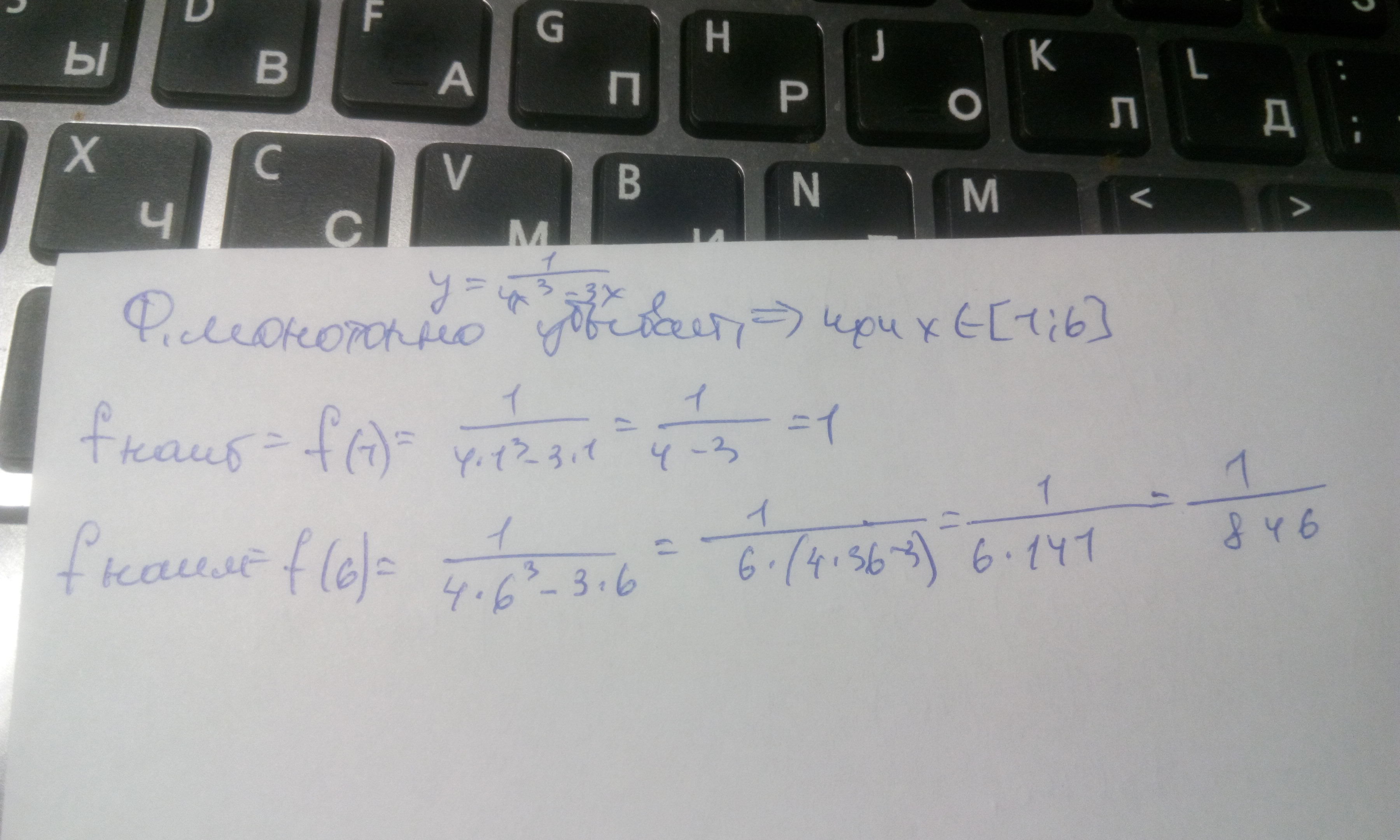
Автор ответа:
0
Спасибо за старания, но условие взяли не то, извиняюсь, что не заметила такой оплошности :(
Автор ответа:
0
Выкладывай фото задания,чтобы можно было понять
Автор ответа:
0
у`=((1/4)·x³ -3x)`=(1/4)·(x³)`-3(x)`=(1/4)·3x²-3;
y`=0
(1/4)·3x²-3=0
3((1/4)x²-1)=0
(1/4)x²-1=0
x²=4
x=2 или х=-2 - точки возможных экстремумов.
-2∉[1;6]
Находим знак производной:
[1]_-__[2]___+____[6]
х=2 - точка минимума функции на [1;6], производная меняет знак с - на +.
у(2)=(1/4)·2³-3·2=2-6=-4 - наименьшее значение функции на [1;6]
Находим значения на концах отрезка
у(1)=(1/4)-3=-2 целых 3/4
у(6)=(1/4)·6³-3·6=54-18=36 - наибольшее значение функции на [1;6]
y`=0
(1/4)·3x²-3=0
3((1/4)x²-1)=0
(1/4)x²-1=0
x²=4
x=2 или х=-2 - точки возможных экстремумов.
-2∉[1;6]
Находим знак производной:
[1]_-__[2]___+____[6]
х=2 - точка минимума функции на [1;6], производная меняет знак с - на +.
у(2)=(1/4)·2³-3·2=2-6=-4 - наименьшее значение функции на [1;6]
Находим значения на концах отрезка
у(1)=(1/4)-3=-2 целых 3/4
у(6)=(1/4)·6³-3·6=54-18=36 - наибольшее значение функции на [1;6]
Приложения:
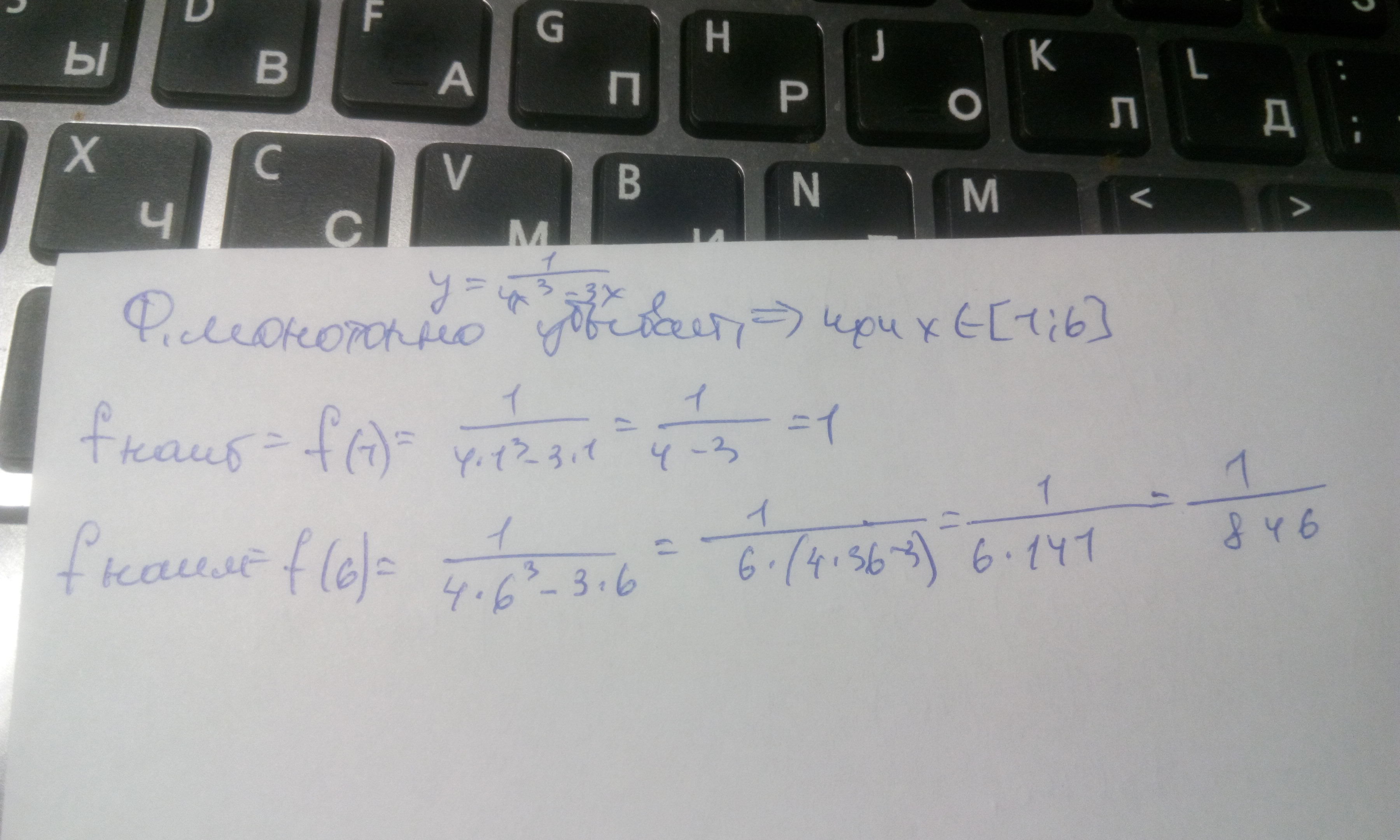
Автор ответа:
0
Благодарю, очень помогли :)
Похожие вопросы
Предмет: Математика,
автор: gribcatovav
Предмет: Математика,
автор: Аноним
Предмет: Французский язык,
автор: bogdanpetrov20
Предмет: География,
автор: Salfetka1