Предмет: Алгебра,
автор: Крис201611
Найдите среднее арифметическое всех корней уравнения
Приложения:
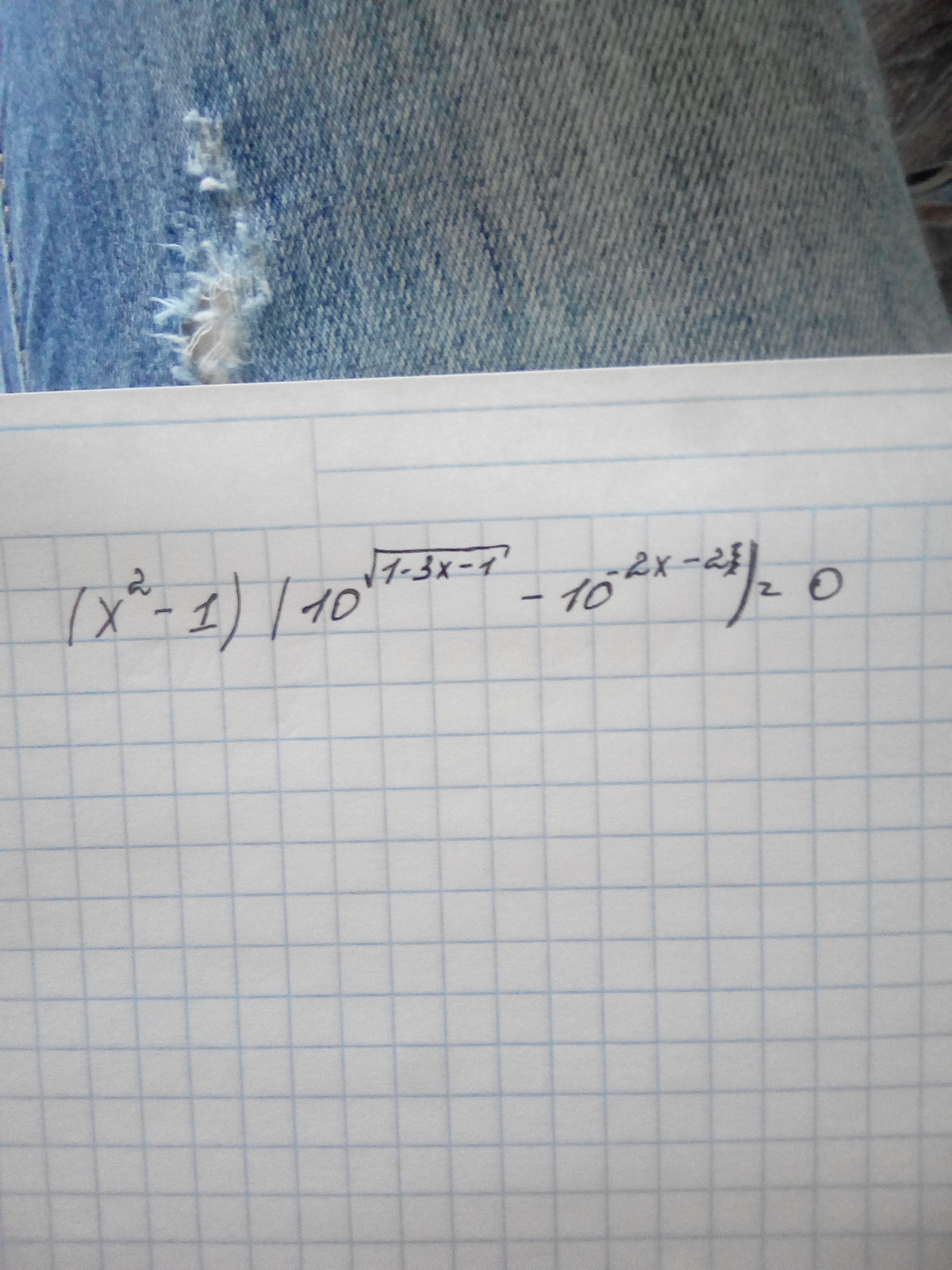
Ответы
Автор ответа:
0
Найдем ОДЗ уравнения.
Произведение равно нулю, значит имеем 2 уравнения
и
Дальше решается как квадратное уравнение.
корни
Среднее арифметическое всех корней уравнения:
Похожие вопросы
Предмет: Литература,
автор: sonyashatrova086
Предмет: Українська мова,
автор: lerakrasotka05
Предмет: Русский язык,
автор: mikayilmusayev500
Предмет: Литература,
автор: polyanskajasch
Предмет: Литература,
автор: Елизавета034