Предмет: Математика,
автор: Dorent
Используя интегральный признак Коши, исследовать на сходимость числовой ряд.
Приложения:
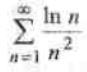
Ответы
Автор ответа:
0
Нужно проинтегрировать выражение
Если интеграл сходится то и ряд будет сходится, если расходится то ряд тоже будет расходится
 интегрируем по частям
интегрируем по частям
 =>
=> 
 =>
=> 
Сама формула интегрирования по частям

Теперь осталось подставить

Вычисляем

Интеграл сходится значит и ряд тоже сходится
Если интеграл сходится то и ряд будет сходится, если расходится то ряд тоже будет расходится
Сама формула интегрирования по частям
Теперь осталось подставить
Вычисляем
Интеграл сходится значит и ряд тоже сходится
Автор ответа:
0
Такие задачи в школе решают?
Автор ответа:
0
Нет это высшая математика
Автор ответа:
0
В предпоследней строке где -lnn/n + 1/n будет -lnn/n - 1/n
Автор ответа:
0
Ответ будет 1 и ряд все равно будет сходится
Похожие вопросы
Предмет: Русский язык,
автор: zamanovazemfira7
Предмет: Алгебра,
автор: podolskaya0619
Предмет: Математика,
автор: nastenkal13
Предмет: История,
автор: katyhayaty27