Предмет: Алгебра,
автор: fubarpatsharp
Здравствуйте, решите, пожалуйста, рациональное неравенство методом интервалов.
Приложения:
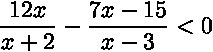
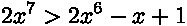
Ответы
Автор ответа:
0
1. 12x / (x+2) = (7x - 15) / (x-3)
2. 12x²-36x=7x²-15x+14x-30
3. 5x²-35x+30=0
4. 5(x²-7x+6)=0
5. 5(x-6)(x-1)=0
x=6 и x=1
подставляешь 7 - получаешь плюс
так как изначальное равенство меньше нуля, то ответ (1;6)
Вторая задача
2x7 = 2x6 - x +1
2x7-2x6+x-1=0
2x6(x-1)+(x-1)=0
(x-1)(2x6+1)=0
x-1=0 x=1 - тут получается, что больше 1 положительно, то есть наш ответ (1;∞)
2x6+1=0 2x6=-1 - тут получается (-∞;∞)
Совмещаем оба и получается ответ (1;∞)
2. 12x²-36x=7x²-15x+14x-30
3. 5x²-35x+30=0
4. 5(x²-7x+6)=0
5. 5(x-6)(x-1)=0
x=6 и x=1
подставляешь 7 - получаешь плюс
так как изначальное равенство меньше нуля, то ответ (1;6)
Вторая задача
2x7 = 2x6 - x +1
2x7-2x6+x-1=0
2x6(x-1)+(x-1)=0
(x-1)(2x6+1)=0
x-1=0 x=1 - тут получается, что больше 1 положительно, то есть наш ответ (1;∞)
2x6+1=0 2x6=-1 - тут получается (-∞;∞)
Совмещаем оба и получается ответ (1;∞)
Автор ответа:
0
вторая задача
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: Merzlyakovr0man
Предмет: Математика,
автор: Z1gZaag
Предмет: Алгебра,
автор: foxy230706
Предмет: Биология,
автор: шk0льник
Предмет: Обществознание,
автор: 20002ангелина2002