Предмет: Математика,
автор: V1nchester
Вычислить определённый интеграл с точностью до второго знака после запятой.
Приложения:
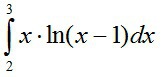
Ответы
Автор ответа:
0
Вводим замену переменной
u=x-1
тогда х=u+1, а du=dx
Получили интеграл

Сначала найдём неопределённый интеграл


Вводим обратную замену








u=x-1
тогда х=u+1, а du=dx
Получили интеграл
Сначала найдём неопределённый интеграл
Вводим обратную замену
Похожие вопросы
Предмет: Математика,
автор: darina6279
Предмет: Математика,
автор: draivovitop123
Предмет: Українська мова,
автор: natalkanikolaeva30
Предмет: Математика,
автор: angellena2