Предмет: Алгебра,
автор: ddrayti
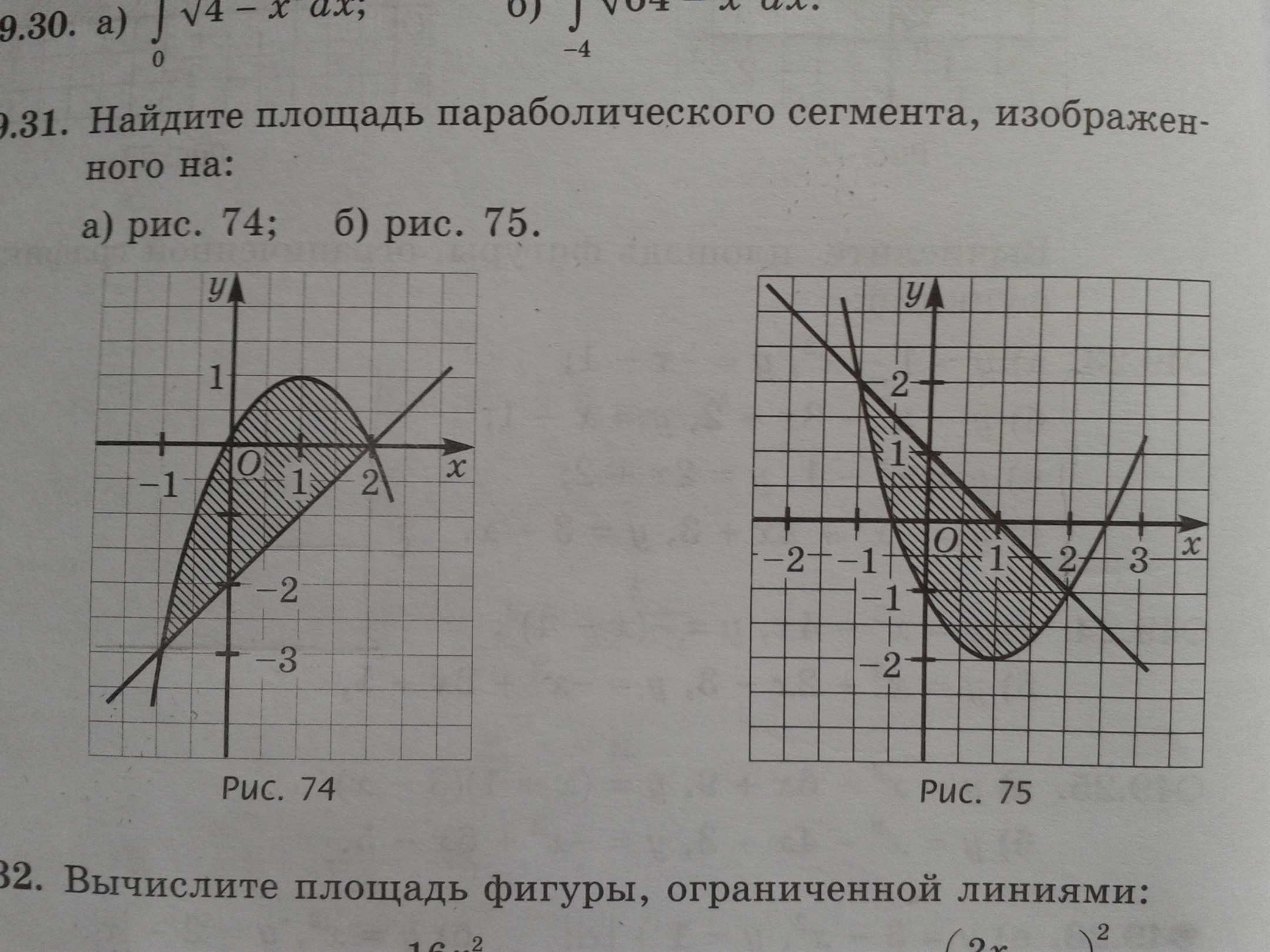
Найдите площадь параболического сегмента
Приложения:
Ответы
Автор ответа:
0
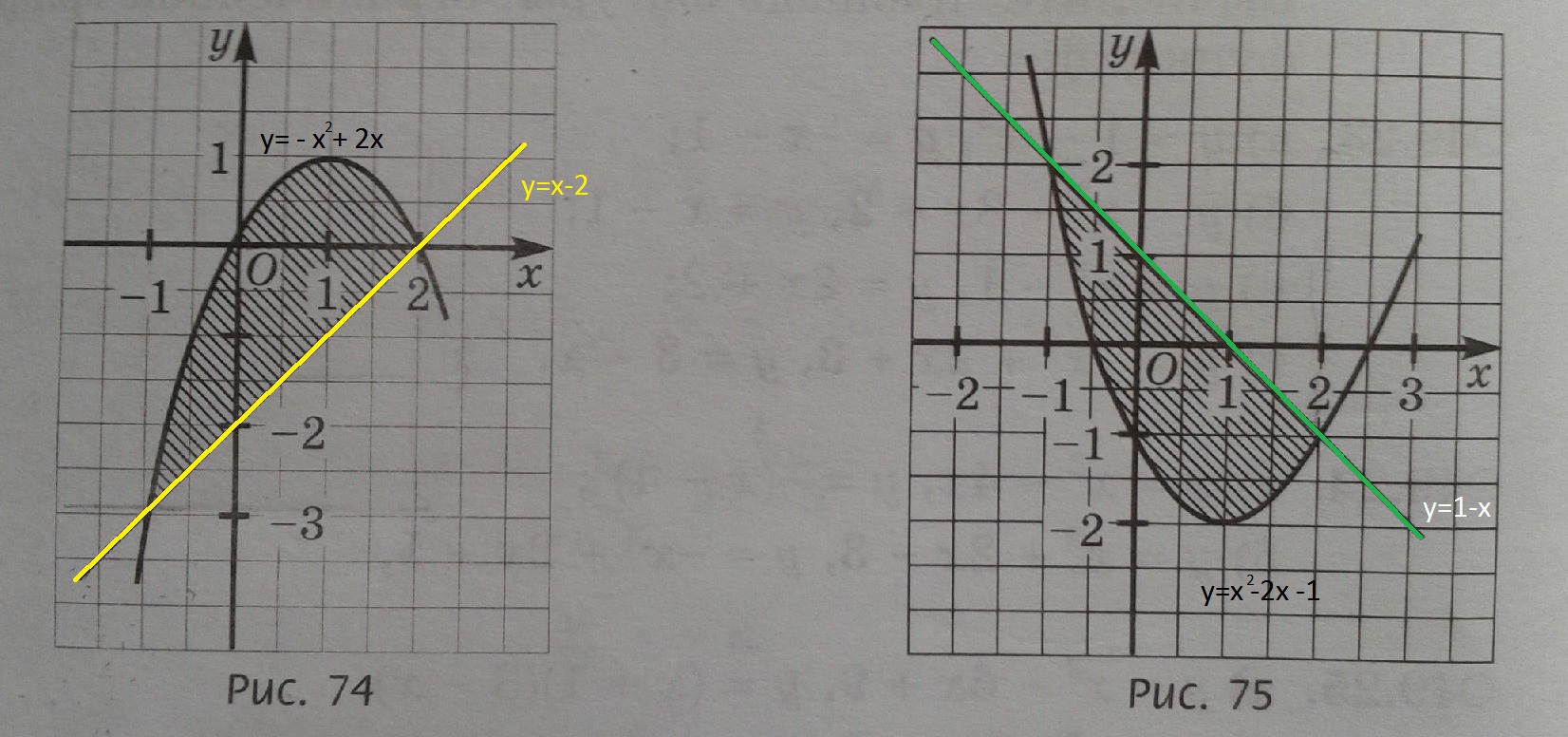
1. Составим уравнение прямой
у=х-2.
Составим уравнение параболы. Ветви параболы направлены вниз, вершина в точке (1;1)
у=-(х-1)²+1
у=-х²+2х

кв. ед.
2.1. Составим уравнение прямой
у = - х+1.
Составим уравнение параболы. Ветви параболы направлены вверх, вершина в точке (1;-2)
у = (х-1)²-2
у = х² - 2х -1

кв. ед.
у=х-2.
Составим уравнение параболы. Ветви параболы направлены вниз, вершина в точке (1;1)
у=-(х-1)²+1
у=-х²+2х
кв. ед.
2.1. Составим уравнение прямой
у = - х+1.
Составим уравнение параболы. Ветви параболы направлены вверх, вершина в точке (1;-2)
у = (х-1)²-2
у = х² - 2х -1
кв. ед.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: imsohappyokey
Предмет: Математика,
автор: sunnysony
Предмет: Русский язык,
автор: izilanovaevgenia
Предмет: Обществознание,
автор: 20002ангелина2002
Предмет: Математика,
автор: 454240