Предмет: Алгебра,
автор: kutsenckosofia
Помогите пожалуйста с решением №13,14
Приложения:
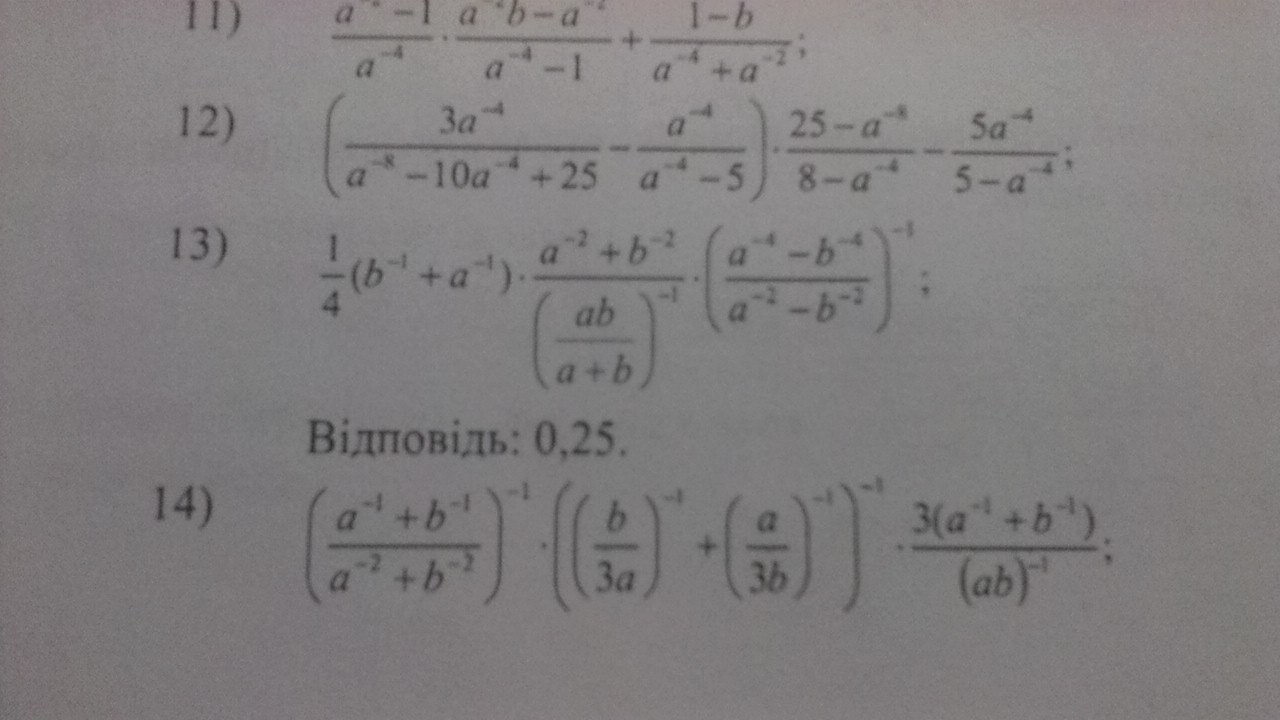
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: romkabazilcuk
Предмет: Математика,
автор: dianashtefaniuk
Предмет: Физика,
автор: roninnnn
Предмет: История,
автор: 1029384756ы
Предмет: Алгебра,
автор: danilkulikov93