Предмет: Математика,
автор: Kharzamanov
Помогите пожалуйста решить задачку.
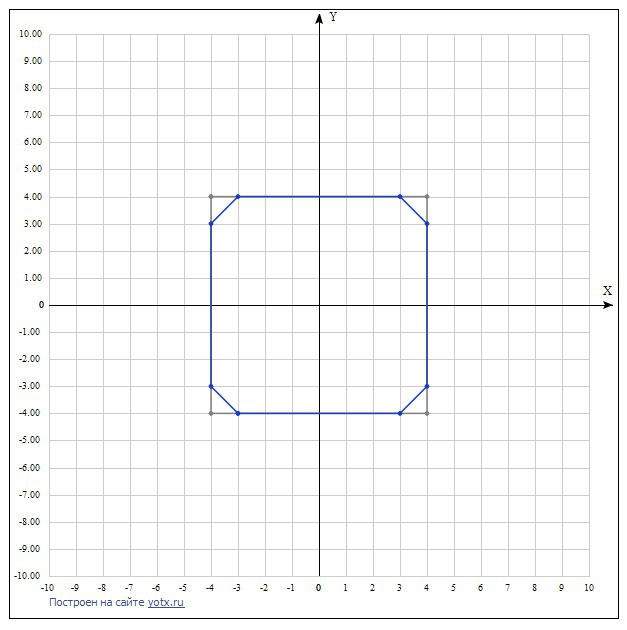
Чему равна площадь восьмиугольника, вершины которого являются решениями системы уравнений:
|x| + |y| = 7
x^2 + y^2 = 25
Ответы
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Математика,
автор: chasnochiQWQ
Предмет: Информатика,
автор: lhelpyou
Предмет: Математика,
автор: Dianallll
Предмет: Алгебра,
автор: shuti99