Предмет: Алгебра,
автор: Оби
пожалуйста помогите. хоть что нибудь
Приложения:
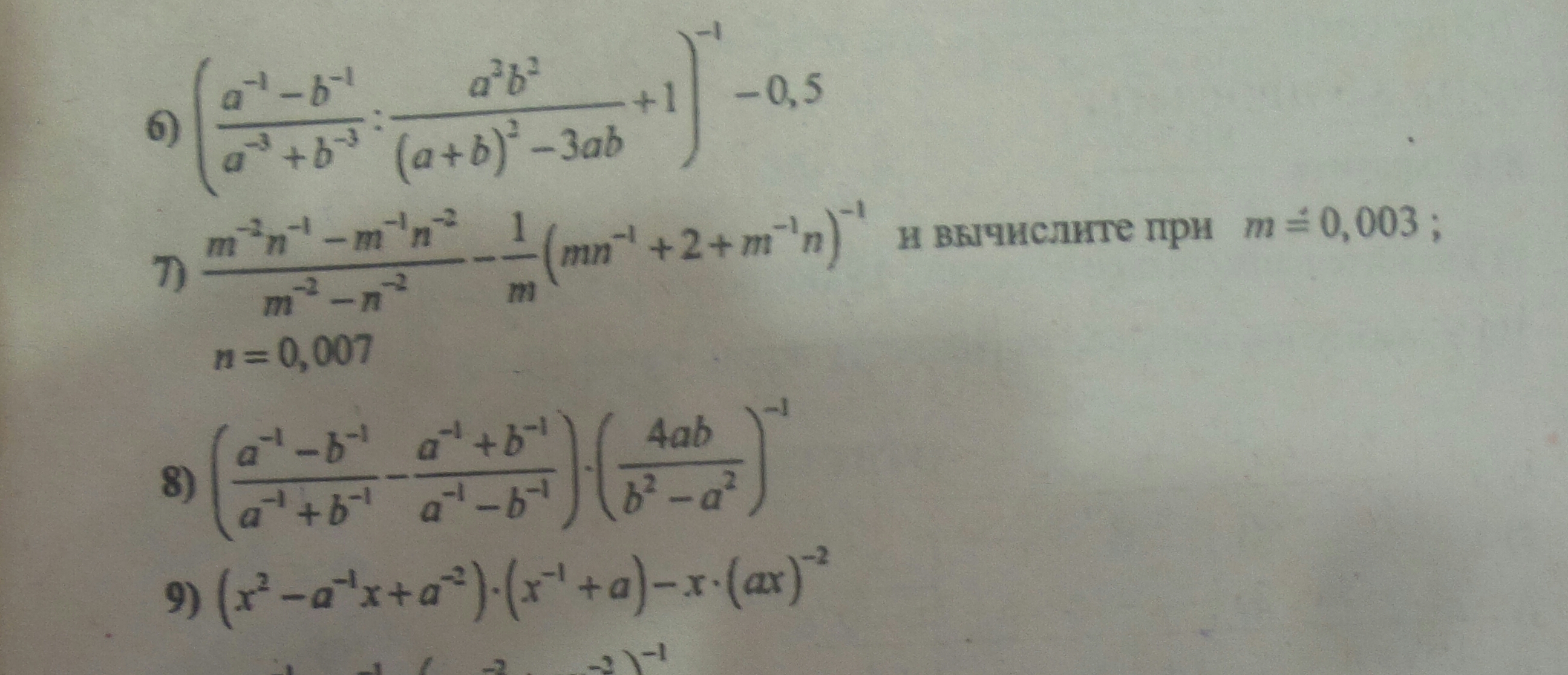
Ответы
Автор ответа:
0
6)


7)


7)
Похожие вопросы
Предмет: Английский язык,
автор: stasjukjulija27
Предмет: Алгебра,
автор: martamuhalyk
Предмет: Алгебра,
автор: Zverin
Предмет: Математика,
автор: kirilllet209
Предмет: География,
автор: dianayata1