Предмет: Математика,
автор: крис517
1. Указать наибольшее целое решение неравенства
х
2 – 8х + 12 < 0
Ответы
Автор ответа:
0
Графиком будет парабола с ветвями вверх. Корни 2 и 6. Отрицательные значения от (2) до (6), значит ответ 5.
5^2-8*5+12=25-40+12=37-40=-3<0
5^2-8*5+12=25-40+12=37-40=-3<0
Автор ответа:
0
Ответ неравенства есть интервал значений икс, при подстановки которых в неравенство оно сохраняется.
Автор ответа:
0
Ответ 5!!! А не от 2 до 6.
Автор ответа:
0
спасиб
Автор ответа:
0
Ответ данного неравенства x∈(2; 6), а вот наибольшее значение средь промежутка сего – пятёрка.
Автор ответа:
0
Квадратные неравенства решаются путём их представления в виде уравнения, нахождения корней и значений икс, принадлежащих промежутку, обусловленному знаком и коэффициентом, стоящим после него. Так,
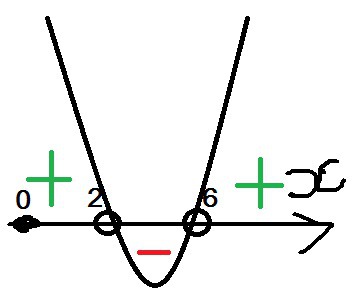
Теперь чертим ось X, отмечаем на ней данные корни и смотрим, при каких значениях икс функция меньше нуля. (График в приложении)
Так как
Ответ: x∈(2; 6)
Приложения:
Автор ответа:
0
О, теперь нормально
Автор ответа:
0
Надо наибольшее целое
Автор ответа:
0
Наибольшее целое решение в промежутке (2; 6)
Автор ответа:
0
это пятёрка
Автор ответа:
0
Вот теперь хорошо!
Похожие вопросы
Предмет: Русский язык,
автор: vhccbf
Предмет: Немецкий язык,
автор: usecodenemorty
Предмет: Алгебра,
автор: anastasiyaline
Предмет: Биология,
автор: leilakorsakova