Предмет: Геометрия,
автор: Marg0ooo
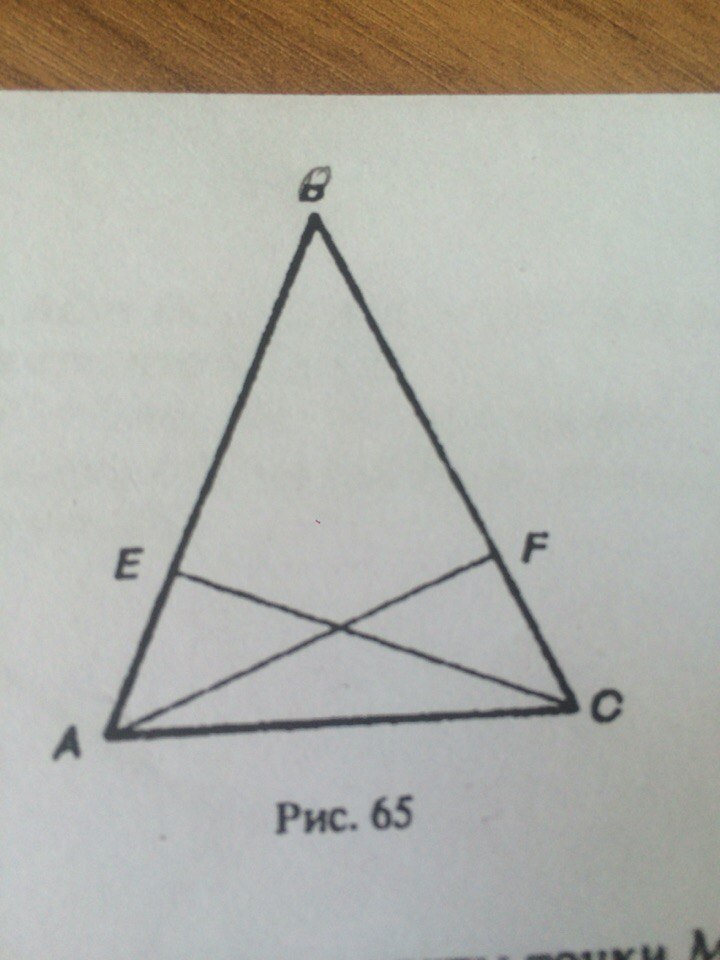
AB=BC
AE=FC
_____________
доказать:
угол AEC= углу AFC
Приложения:
Ответы
Автор ответа:
0
Доказательство.
Для доказательство данного утверждение необходимо и достаточно доказать, что треугольники AEC и AFC равны. Действительно, они равны по первому признаку равенства треугольников: EA=FC по условию, сторона AC - общая, а углы EAC и FCA равны как углы при основании AC равнобедренного треугольника ABC (AB=BC по условию). Из равенства данных треугольников следует: углы AEC и AFC равны. Что и требовалось доказать.
Для доказательство данного утверждение необходимо и достаточно доказать, что треугольники AEC и AFC равны. Действительно, они равны по первому признаку равенства треугольников: EA=FC по условию, сторона AC - общая, а углы EAC и FCA равны как углы при основании AC равнобедренного треугольника ABC (AB=BC по условию). Из равенства данных треугольников следует: углы AEC и AFC равны. Что и требовалось доказать.
Автор ответа:
0
"а углы EAC и FCA равны" - доказать это также прийдется, углы при основании, это BAC, BCA
Автор ответа:
0
Это одни и те же углы как бы. Можно, разве что, указать, что, например, Е принадлежит... и т.д.
Автор ответа:
0
как бы нет, это части углов при основании. смысл задачи показать, что радиусом FC или AE из точет равноудаленных от вершины на противоположной стороне угла отсекаются равные отрезки AF и EC
Автор ответа:
0
ВАС=ВСА, равнобедренный треугольник
АЕ=FC, AC = CA на сторонах равных углов ВАС, BCA, отсекают равные отрезки AF=EC
треугольники равны AEC=AFC по двум сторонам и углу между ними, соответсвенно равны все элементы равных треугольников, т.е. углы AFC=AEC
АЕ=FC, AC = CA на сторонах равных углов ВАС, BCA, отсекают равные отрезки AF=EC
треугольники равны AEC=AFC по двум сторонам и углу между ними, соответсвенно равны все элементы равных треугольников, т.е. углы AFC=AEC
Похожие вопросы
Предмет: Английский язык,
автор: sofikopach
Предмет: Английский язык,
автор: stasjukjulija27
Предмет: Алгебра,
автор: martamuhalyk
Предмет: Литература,
автор: natusia369