Предмет: Математика,
автор: Аноним
Ребят помогите пожалуйста, хотябы по 5 заданий с каждой фотки. 90 Баллов даю. Без кидалова ток... до 21:00 надо.
Приложения:

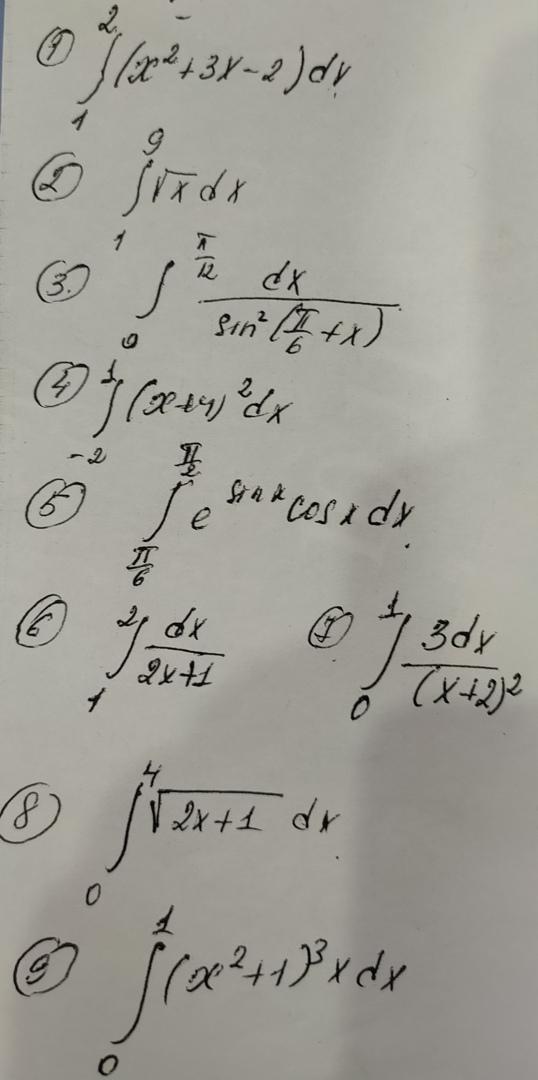
Miroslava227:
сколько времени осталось?
я решаю уже , минут 30 будет готово
Ответы
Автор ответа:
1
Ответ:
1.
2
3
4
5
6
7
____________________
1
2
3
4
5
6
7
8
Похожие вопросы
Предмет: Қазақ тiлi,
автор: riga2004
Предмет: Русский язык,
автор: алисаКуш
Предмет: Русский язык,
автор: сегодня3
Предмет: Окружающий мир,
автор: 42ррау7шн
Предмет: Химия,
автор: LectorFreeze4680