Предмет: Математика,
автор: MeShootIn
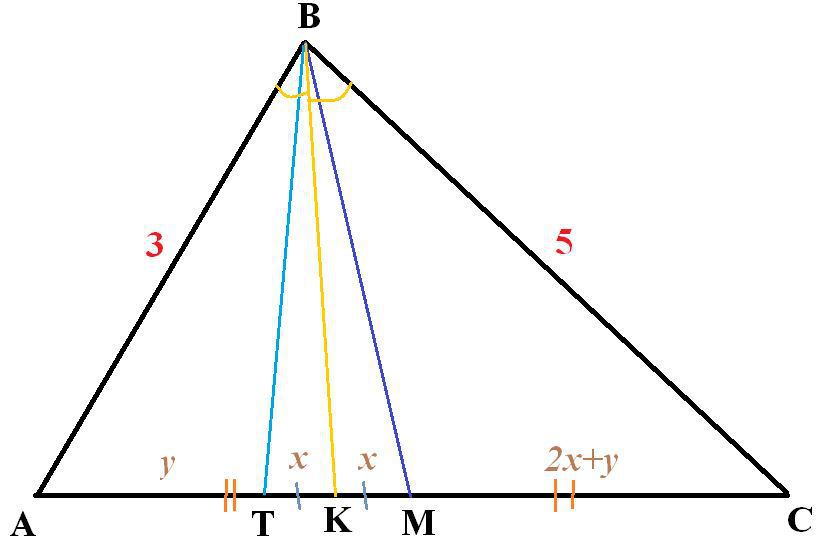
В треугольнике АВС АВ=3, ВС=5. BM - медиана, BK - биссектриса. Прямая ВТ симметрична BM относительно BK, причем T лежит на стороне АС. Чему равно отношение АТ:СТ?
Ответы
Автор ответа:
0
Чертеж - во вложении.
ВМ - медиана Δ АВС ⇒ АМ=СМ.
ВК - биссектриса Δ АВС ⇒ АК:КС=3:5.
Прямая ВТ симметрична BM относительно BK ⇒ КТ=МТ.
Пусть КТ=МТ=х, АТ=у, тогда МС=АМ=2х+у

5x+5y=9x+3y
2y=4x
y=2x ⇒ T - середина АМ ⇒ AT=TM=2x, MC=2x+2x=4x.
⇒ TC =TM+MC = 2x+4x=6x

Ответ: 1:3.
ВМ - медиана Δ АВС ⇒ АМ=СМ.
ВК - биссектриса Δ АВС ⇒ АК:КС=3:5.
Прямая ВТ симметрична BM относительно BK ⇒ КТ=МТ.
Пусть КТ=МТ=х, АТ=у, тогда МС=АМ=2х+у
5x+5y=9x+3y
2y=4x
y=2x ⇒ T - середина АМ ⇒ AT=TM=2x, MC=2x+2x=4x.
⇒ TC =TM+MC = 2x+4x=6x
Ответ: 1:3.
Приложения:
Автор ответа:
0
там опечатка КТ=КМ=х. Но в ответе из-за нее ничего не должно измениться
Автор ответа:
0
должно я знаю что 1 к 4 - неправильный ответ
Автор ответа:
0
и 1 к 3 тоже
Автор ответа:
0
вы правы. я не закончил решение, не дописал последнее равенство. нажмите возле моего ответа кнопку НАРУШЕНИЕ. модераторы отправят мне на исправление
Автор ответа:
0
так всё равно ж неправильно(
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: polino4ka1508
Предмет: Математика,
автор: sumbaevaksenia64
Предмет: Математика,
автор: gilevakaso