Предмет: Алгебра,
автор: kmdnc
решите 34 или 35 нер-во
Приложения:
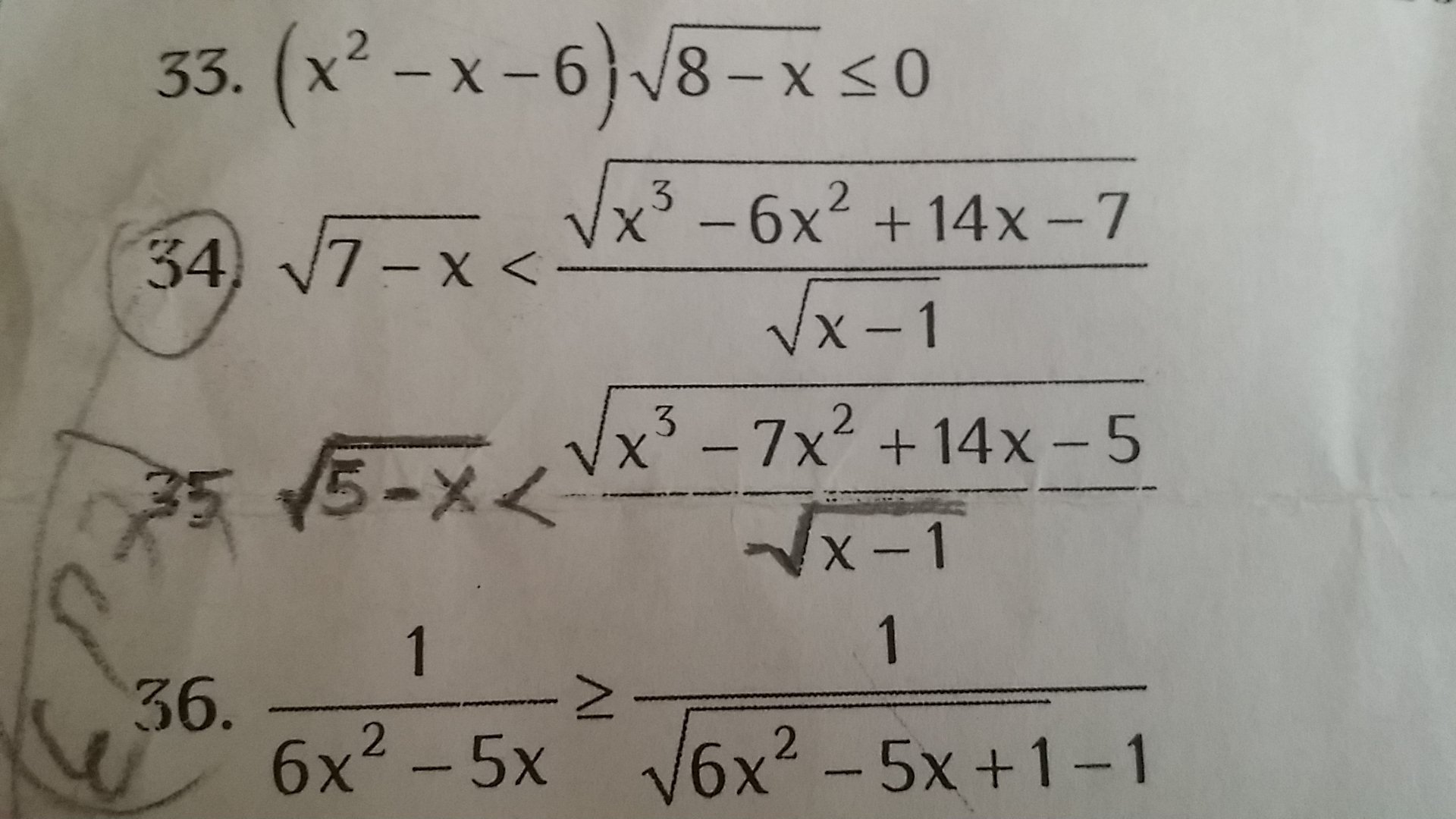
Ответы
Автор ответа:
0
34. ОДЗ корня в левой части и корня в знаменателе дроби: 1<x≤7
Теперь домножаем неравенство на знаменатель:

Все, теперь корни можно отбросить и перейти к неравенству
x³-6x²+14x-7>(x-1)(7-x). Ведь (x-1)(7-x)>0 на одз, поэтому левая часть уж точно будет положительна.
x³-6x²+14x-7>-x^2+8x-7
x³-5x²+6x>0
x(x²-5x+6)>0
x(x-3)(x-2)>0
(0; 2)∪(3;+oo)
Пересекая это решение с одз получаем:
(1; 2) ∪ (3; 7]
35 решается таким же способом.
Теперь домножаем неравенство на знаменатель:
Все, теперь корни можно отбросить и перейти к неравенству
x³-6x²+14x-7>(x-1)(7-x). Ведь (x-1)(7-x)>0 на одз, поэтому левая часть уж точно будет положительна.
x³-6x²+14x-7>-x^2+8x-7
x³-5x²+6x>0
x(x²-5x+6)>0
x(x-3)(x-2)>0
(0; 2)∪(3;+oo)
Пересекая это решение с одз получаем:
(1; 2) ∪ (3; 7]
35 решается таким же способом.
Похожие вопросы
Предмет: История,
автор: Finet
Предмет: Русский язык,
автор: kfjlmkjlkdyhktrl
Предмет: Английский язык,
автор: nastyaruzchakk
Предмет: Математика,
автор: ikizli2011
Предмет: Алгебра,
автор: yapolinadim