Question

Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 30 градусов. Найдите объем конуса

Answer 1

Рисунок прикреплен.

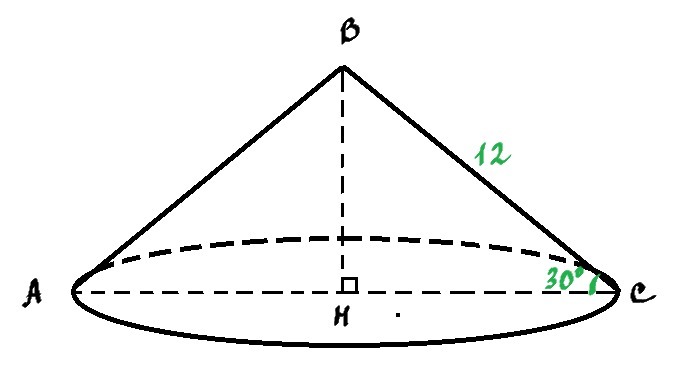
Дано: конус, ВС=12 см, ∠НСВ=30°

Найти: объем конуса

Решение: по условию образующая конуса наклонена к плоскости под углом в 30°. Это значит, что угол между образующей и радиусом основания конуса 30°.

Из вершины конуса опустим высоту. Обозначим её ВН.

ΔВНС прямоугольный.

У него известна гипотенуза ВС=12 и ∠НСВ=30°.

В прямоугольном треугольнике катет, лежащий напротив угла в 30° в два раза меньше гипотенузы.

$BH=frac{BC}{2}=frac{12}{2}=6$

По теореме Пифагора найдем второй катет ΔВНС. Он же является радиусом основания конуса.

$HC=sqrt{BC^2-BH^2}=sqrt{12^2-6^2}=sqrt{144-36}=sqrt{108}$

Объем конуса вычисляется по формуле: $V=frac{1}{3}pi R^2h$, где R - радиус основания, h - высота конуса.

$V=frac{1}{3}pi R^2h=frac{1}{3}pi (sqrt{108})^2*6 =108*2pi =216pi$

Ответ: 216π см³