Предмет: Математика,
автор: vovanata
докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям и равен их полуразности.
Ответы
Автор ответа:
0
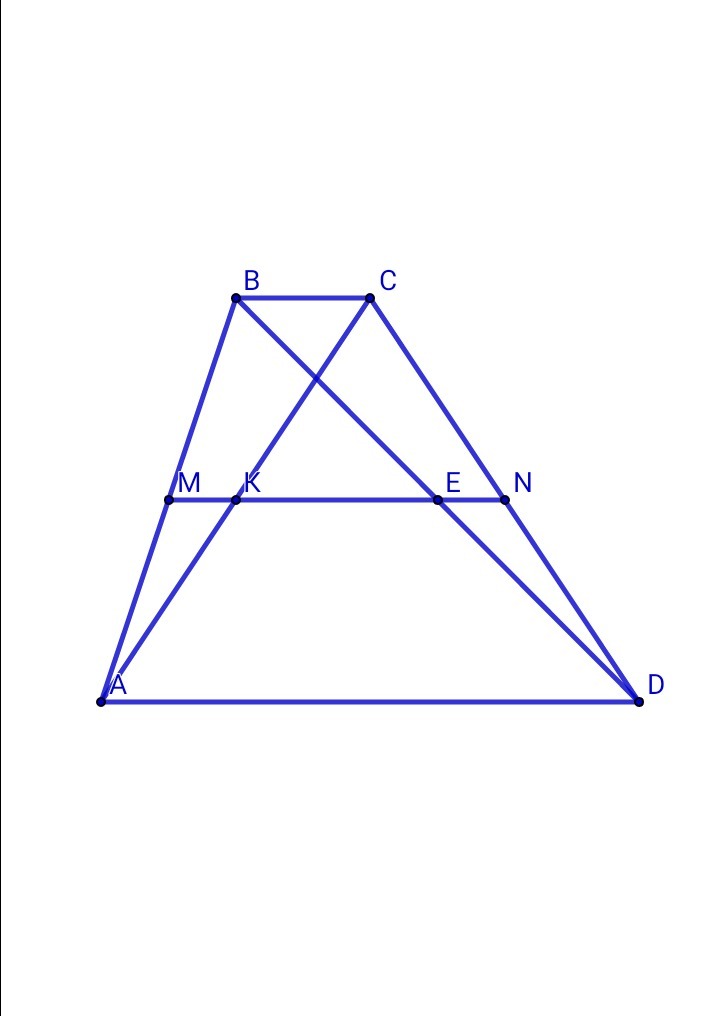
Пусть AM = MB , CN = ND ⇒ MN - средняя линия, MN || ВС || AD
По теореме Фалеса AK = KC , BE = ED ⇒ KE - отрезок, соединяющий середины диагоналей трапеции
В ΔBAD: AМ = МВ , ВЕ = ED ⇒ ME - средняя линия
ME = AD/2
В ΔABC: AM = MB , AK = KC ⇒ MK - средняя линия
МК = ВС/2
КЕ = МЕ - МК = AD/2 - BC/2 = ( AD - BC )/2 , что и требовалось доказать
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Margo040801
Предмет: Биология,
автор: vanyasekushin
Предмет: Литература,
автор: egor4ik0511