Предмет: Математика,
автор: KaTTasTrofa
Помогите решить,желательно подробно,не могу понять.
Приложения:
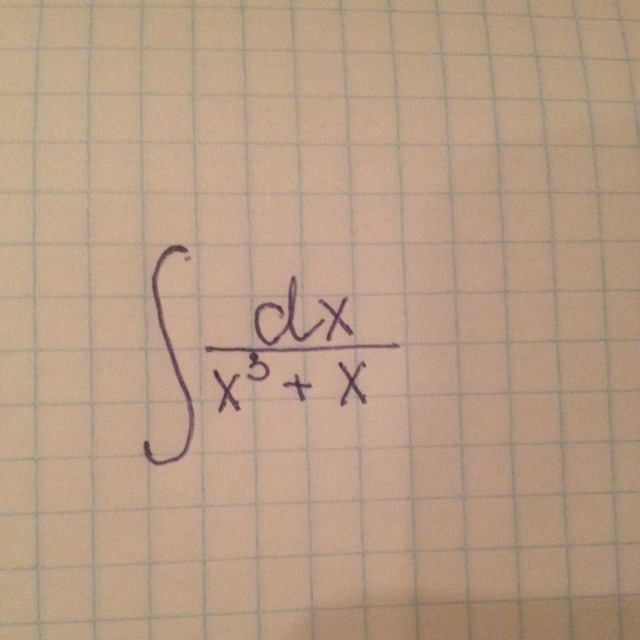
Ответы
Автор ответа:
0
разложим дробь на сумму элементарных дробей с помощью метода неопределенных коэффициентов
1/(x³+x)=1/x(x²+1)=A/x+Bx/(x²+1)
(Ax²+A+Bx²)/x(x²+1)=1/x(x²+1)
x²(A+B)+A=1
A+B=0
A=1
B=-A=-1
таким образом
1/(x³+x)=1/x-x/(x²+1)
∫dx/(x³+x)=∫[1/x-x/(x²+1)]dx=∫dx/x-∫xdx/(x²+1)
вычислим каждый интеграл отдельно
1)∫dx/x=ln/x/+с, ( /x/ это модуль х )
2) во втором интеграле внесем х под знак дифференциала
xdx=(1/2)dx²=(1/2)d(x²+1)
∫xdx/(x²+1)=∫(1/2)dx²/(x²+1)=(1/2)∫(d(x²+1))/(x²+1)= обозначим x²+1=y
=(1/2)∫(1/y)dy=(1/2)lny+с=(1/2)ln(x²+1)+с
сложим оба интеграла
ln/x/-(1/2)ln(x²+1)+с
проверка
(ln/x/-(1/2)ln(x²+1))'=1/x-(1/2)*2x/(x²+1)=1/x-x/(x²+1)=(x²+1-x²)/x(x²+1)= 1/x(x²+1)=1/(x³+x)
1/(x³+x)=1/x(x²+1)=A/x+Bx/(x²+1)
(Ax²+A+Bx²)/x(x²+1)=1/x(x²+1)
x²(A+B)+A=1
A+B=0
A=1
B=-A=-1
таким образом
1/(x³+x)=1/x-x/(x²+1)
∫dx/(x³+x)=∫[1/x-x/(x²+1)]dx=∫dx/x-∫xdx/(x²+1)
вычислим каждый интеграл отдельно
1)∫dx/x=ln/x/+с, ( /x/ это модуль х )
2) во втором интеграле внесем х под знак дифференциала
xdx=(1/2)dx²=(1/2)d(x²+1)
∫xdx/(x²+1)=∫(1/2)dx²/(x²+1)=(1/2)∫(d(x²+1))/(x²+1)= обозначим x²+1=y
=(1/2)∫(1/y)dy=(1/2)lny+с=(1/2)ln(x²+1)+с
сложим оба интеграла
ln/x/-(1/2)ln(x²+1)+с
проверка
(ln/x/-(1/2)ln(x²+1))'=1/x-(1/2)*2x/(x²+1)=1/x-x/(x²+1)=(x²+1-x²)/x(x²+1)= 1/x(x²+1)=1/(x³+x)
Похожие вопросы
Предмет: Математика,
автор: KsushenkaCute
Предмет: Химия,
автор: Taninan
Предмет: Українська мова,
автор: vovaklai
Предмет: Математика,
автор: ариночкин