Предмет: Математика,
автор: L7atruot
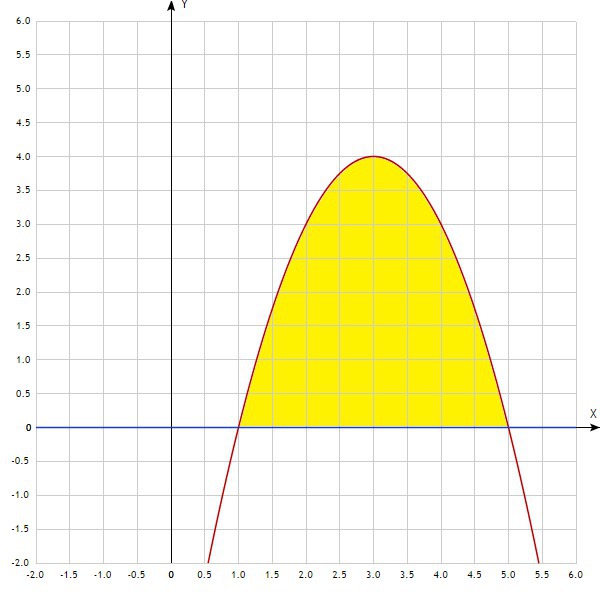
Найти площадь фигуры ограниченной линиями y=-x^2+6x-5 y=0
Ответы
Автор ответа:
0
Находим пределы интегрирования
-x²+6x-5=0
D=6²-4*(-1)*(-5)=36-20=16
x=(-6-4)/-2=5 x=(-6+4)/-2=1


 ед²
ед²
-x²+6x-5=0
D=6²-4*(-1)*(-5)=36-20=16
x=(-6-4)/-2=5 x=(-6+4)/-2=1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sofiagrabovskaj
Предмет: Математика,
автор: vlad93747
Предмет: Английский язык,
автор: zinkivskan
Предмет: Математика,
автор: deni567
Предмет: Математика,
автор: lexiy21