Question

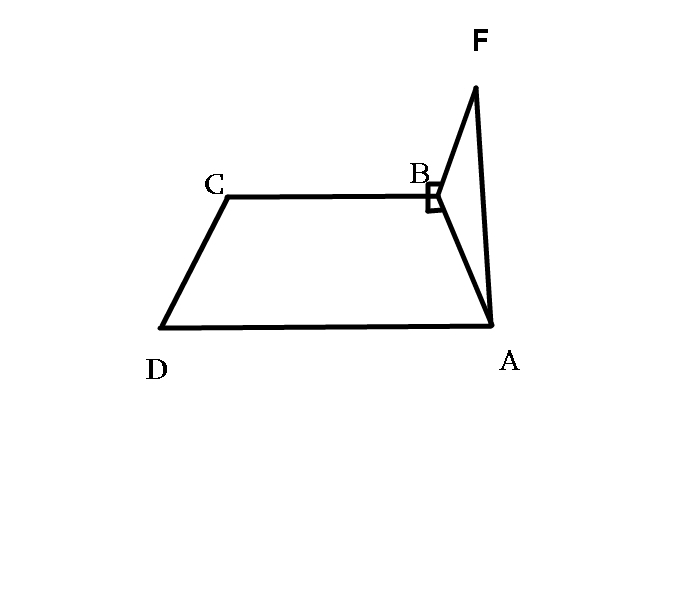
1. Дана трапеция ABCD , в которой AD||BC и AB перпендикулярна CB . Через вершину B проведена прямая F, которая не лежит в плоскости трапеции и перпендикулярная прямой BC .Докажите , что прямая BC перпендикулярная плоскости ABF.
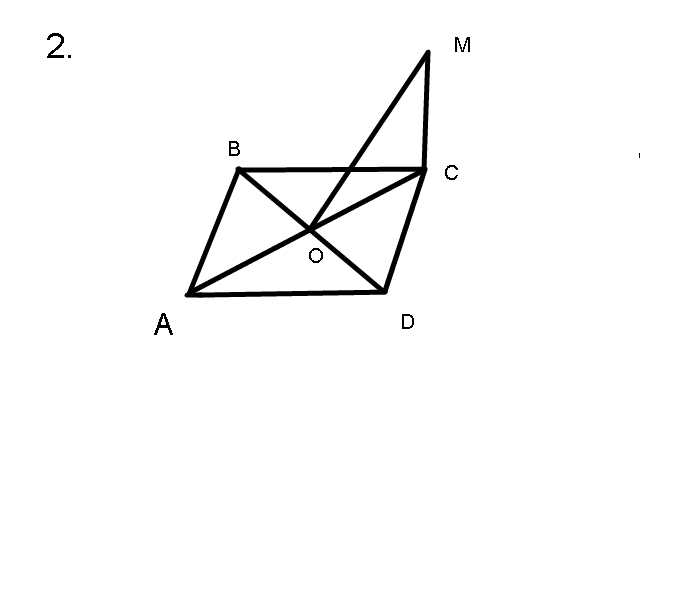
2. Через вершину С квадрата ABCD проведена прямая MC, которая перпендикулярна плоскости квадрата AC∩BD=O
1)Докажите что прямые BD и MO перпендикулярны
2)Вычислить расстояния от т.M до прямой BD , если MC = 1 cм , СD= 4 см

Answer 1

1
АВ_|_BС U AB_|_BF⇒BC_|_BF
BF∈(ABF)⇒BC_|_(ABF)
Если прямая перпендикулярна прямой,лещащей в плоскости,то она перпендикулярна и самой плоскости.
2
МС_|_(ABC) U MC∈(MCO)⇒(ABC)_|_(MCO)
BD∈(ABC) U MO∈(MCO)⇒BD_|_MO
Если плоскости перпендикулярны,то и прямые ,лежащие в этих плоскостях перпендикулярны.

Answer 2

Извините, но вчера я не мог Вам помочь. Первая решена верно. решение второй  в скане...........