Question

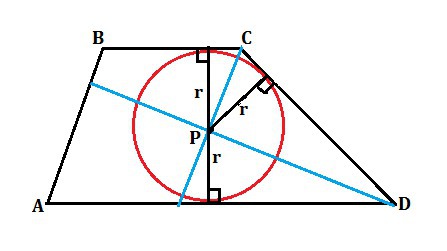
В тропеции ABCD точка P расположена на пересечении биссектрис C и D, докажите что точка P равноудалена от прямых BC, AD, CD.

Answer 1

В трапеции АВСД биссектрисы углов С и Д пересекаются в точке Р. 
Проведём перпендикуляры РК, РН и РМ к сторонам ВС, СД и АД соответственно.
Треугольники КРС и НРС равны, так как ∠КСР=∠НСР, оба прямоугольные и сторона СР - общая, значит КР=НР. 
Аналогично доказывается равенство тр-ков НРД и МРД. В них МР=НР.
Доказано,что КР=НР=МР, задача решена.

Answer 2

Вариант решения. 
Центр вписанной в угол окружности лежит на его биссектрисе. 
Центром вписанной в угол С и угол D  окружности будет точка пересечения их биссектрис. 
Расстоянием от Р до прямых ВС, AD и CD будет длина перпендикуляра из Р до данных прямых, т.е. радиус этой окружности, а его величина постоянна.
Следовательно, точка Р - равноудалена от прямых CD, AD, CD.