Question

Найдите площадь фигуры,ограниченной прямой y=1-2x и графиком функции y=x^2-5x-3

Answer 1

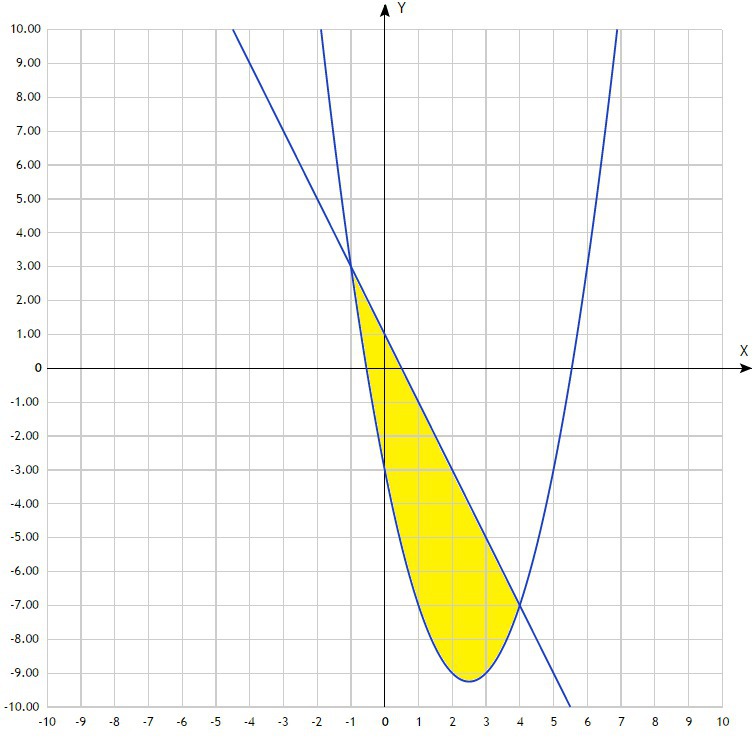
Для наглядности и определения точек пересечения линий графиков функций делаем чертёж. Из чертежа видим, что линии графиков пересекаются в точках х=-1 и х=4, значит нижний предел интегрирования а=-1, верхний предел интегрирования b=4. Их также можно найти аналитически, решив уравнение
x²-5x-3=1-2x
x²-5x+2x-3-1=0
x²-3x-4=0
D=(-3)²-4*(-4)=9+16=25
x=(3-5)/2=-1   x=(3+5)/2=4
Из рисунка также видно, что прямая расположена выше параболы, а значит для нахождения площади необходимо в формулу площади
$S= intlimits^b_a {(f(x)-g(x))} , dx$
вместо f(x) подставить (1-2х), а вместо g(x) подставить (x²-5x-3):
$S= intlimits^4_{-1} {((1-2x)-(x^2-5x-3))} , dx = intlimits^4_{-1} {(-x^2+3x+4)} , dx =$
$=- frac{x^3}{3}+ frac{3x^2}{2}+4x|_{-1}^{4}=$
$=- frac{4^3}{3}+ frac{3*4^2}{2}+4*4-(- frac{(-1)^3}{3}+ frac{3*(-1)^2}{2}+4*(-1))=$
$=- frac{64}{3} +24+16-( frac{1}{3}+1-4)= - frac{68}{3} +44=21 frac{1}{3}$ ед²