Предмет: Математика,
автор: 111ii
Пожалуйста, помогите с заданием :с
1) Исследуйте функцию f(x)=3x2-x^3 по следующей схеме:
1. Область определения.
2.Точки пересечения графика с осями координат.
3.Промежутки возрастания и убывания.
4.Экстремумы
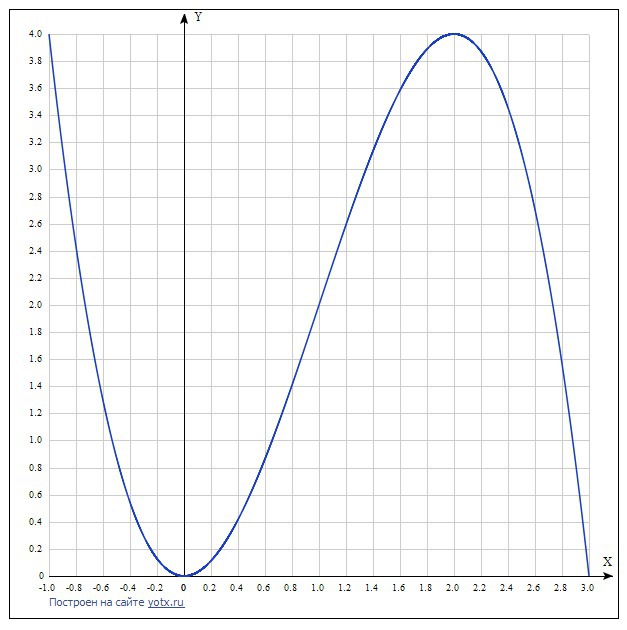
Постройте график данной функции.
2) Найдите наибольшее и наименьшее значения функции y= -x^3-3x^2+9-2 на отрезке [-2;2]
Очень буду благодарна за вашу помощь!
Ответы
Автор ответа:
0
Функция f(x)=3x²-x³
1. Область определения - нет ограничений D(f) = R.
2.Точки пересечения графика с осями координат.
При х = 0, у = 0 точка пересечения с осью Оу.
При 3x²-x³ = 0, x²(3 - х) = 0 есть 2 точки пересечения с осью Ох: х = 0 и х = 3.
3.Промежутки возрастания и убывания.
Находим производную функции и приравниваем её 0:
f'(3x²-x³) = 6x - 3x² = 3x(2 - x) = 0.
Нашли 2 критические точки:
х = 0 и х = 2.
Находим знаки производной вблизи критических точек:
х = -0.5 0 1.5 2 2.5
у' =6x - 3x² = -3.75 0 2.25 0 -3.75 .
Где производная отрицательна - там функция убывает, где производная положительна - функция возрастает.
x < 0 и x > 2 функция убывает,
0 < x < 2 функция возрастает.
4.Экстремумы видны по пункту 3. Где производная меняет знак с - на + там минимум, где с + на - там максимум:
х = 0 минимум, х = 2 максимум.
1. Область определения - нет ограничений D(f) = R.
2.Точки пересечения графика с осями координат.
При х = 0, у = 0 точка пересечения с осью Оу.
При 3x²-x³ = 0, x²(3 - х) = 0 есть 2 точки пересечения с осью Ох: х = 0 и х = 3.
3.Промежутки возрастания и убывания.
Находим производную функции и приравниваем её 0:
f'(3x²-x³) = 6x - 3x² = 3x(2 - x) = 0.
Нашли 2 критические точки:
х = 0 и х = 2.
Находим знаки производной вблизи критических точек:
х = -0.5 0 1.5 2 2.5
у' =6x - 3x² = -3.75 0 2.25 0 -3.75 .
Где производная отрицательна - там функция убывает, где производная положительна - функция возрастает.
x < 0 и x > 2 функция убывает,
0 < x < 2 функция возрастает.
4.Экстремумы видны по пункту 3. Где производная меняет знак с - на + там минимум, где с + на - там максимум:
х = 0 минимум, х = 2 максимум.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: mariannamarjassova
Предмет: Английский язык,
автор: olyasochnk
Предмет: Информатика,
автор: Аноним
Предмет: Литература,
автор: Dianalovenya
Предмет: Математика,
автор: xenusxxx77