Предмет: Алгебра,
автор: MAPNR
Найти наименьшее значение x^2+y^2,
если x+|y| больше или равно корню из 6
Ответы
Автор ответа:
0
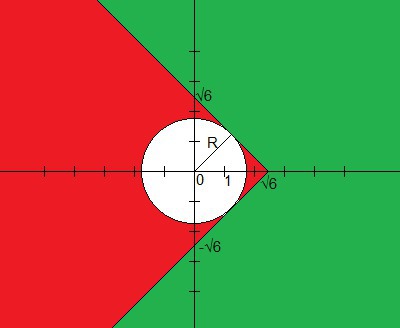
Изобразим область x+|y| <=√6. На рисунке она выделена зеленым цветом.Изобразим на графике окружность радиуса R c центром в (0;0). Квадрат радиуса будет равен значению x^2 + y^2. Будем увеличивать радиус окружности до тех пор, пока она не коснется границ зеленой области. Квадрат радиуса в таком случае как раз и будет ответом - наименьшим значением x^2+y^2 при x+|y| <=√6. Найдем радиус. В прямоугольном треугольнике, который ограничен осями координат и верхней диагональной границей зеленой области, высота из прямого угла совпадает с радиусом окружности. Треугольник равнобедренный, катеты его равны √6. Следовательно, высота равна √6 / √2 = √3 (при рассмотрении более маленького треугольника, у которого гипотенуза равна √6, а высота большого треугольника - один из его катетов). Тогда радиус равен √3, а квадрат радиуса равен 3.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ilaivanov509
Предмет: Оʻzbek tili,
автор: malika060891
Предмет: География,
автор: Svolochyyyy5
Предмет: Химия,
автор: Sabina99good
Предмет: Алгебра,
автор: Nataliashiroko