Предмет: Алгебра,
автор: Аноним
помогите решить пожалуйста
Приложения:
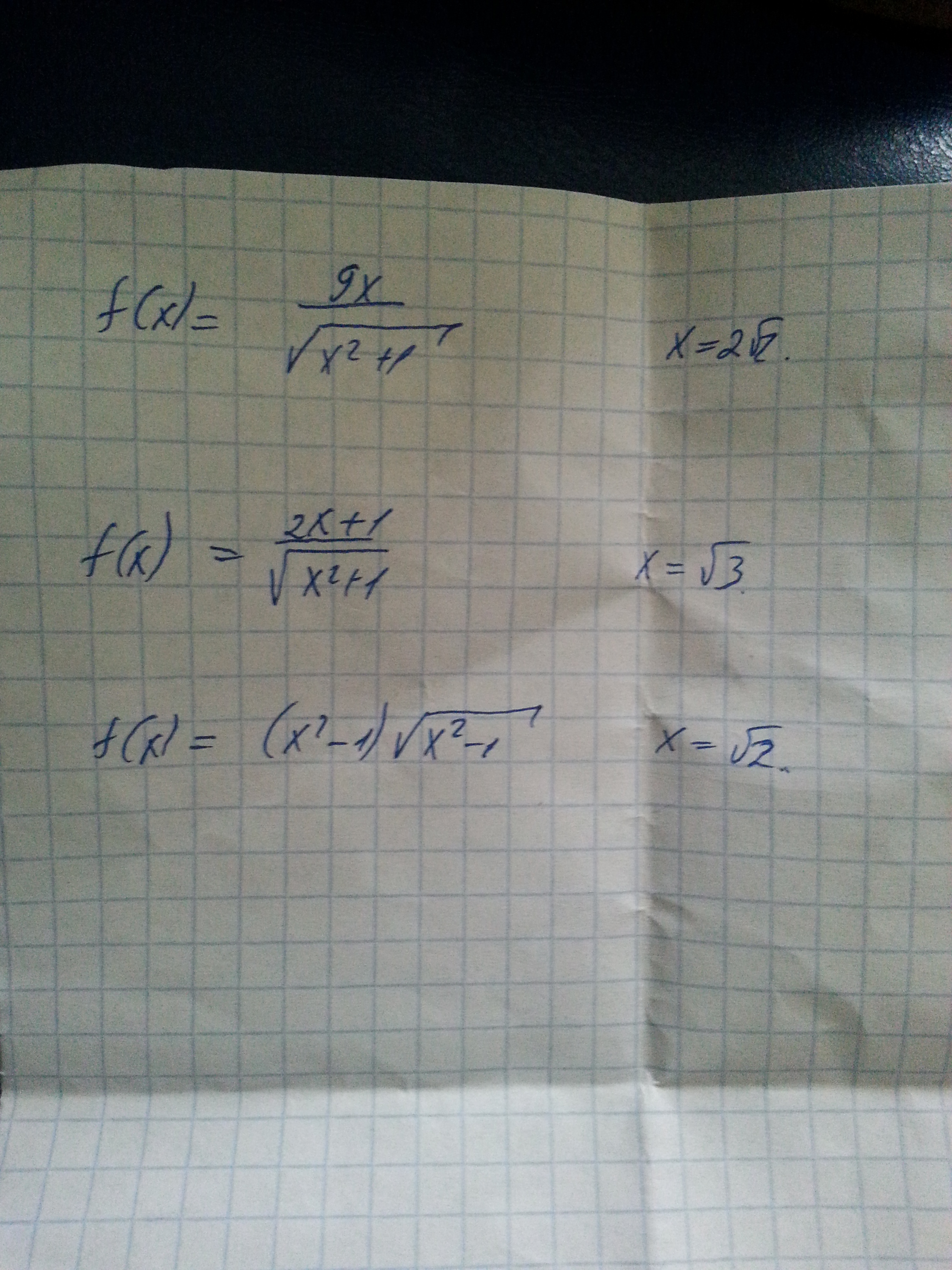
Ответы
Автор ответа:
0
1) 


2)



3)


2)
3)
Похожие вопросы
Предмет: Українська мова,
автор: Jjjjjjjj2q
Предмет: Алгебра,
автор: valikrybka0
Предмет: Алгебра,
автор: MamondaBrainMaps
Предмет: Литература,
автор: kristinasat