Предмет: Алгебра,
автор: DerЗзКий
Вычислите площадь фигуры, ограниченной заданными линиями. Выполните рисунки.
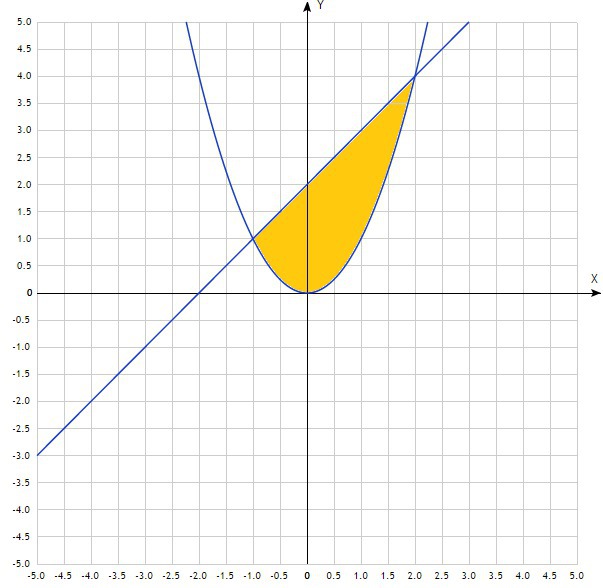
1) y = x²; y = x+2
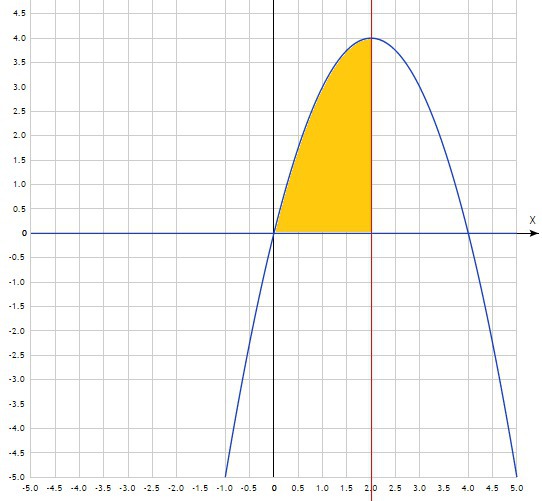
2) y = -x²+4x; x = 2; y = 0
Ответы
Автор ответа:
0
1) Искомая фигура ограничена прямой сверху и параболой снизу (как видно из рисунка) на отрезке [-1;2]

 ед²
ед²
Ответ: S=4,5 ед²
2) Искомая фигура ограничена сверху параболой, снизу прямой, совпадающей с осью ОХ на отрезке [0;2]

 ед²
ед²
Ответ: S=16/3 ед²
Ответ: S=4,5 ед²
2) Искомая фигура ограничена сверху параболой, снизу прямой, совпадающей с осью ОХ на отрезке [0;2]
Ответ: S=16/3 ед²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: arinapetrosyan23
Предмет: Химия,
автор: Birulyka
Предмет: Биология,
автор: anasadvarij67
Предмет: Литература,
автор: Lesha01