Предмет: Математика,
автор: pro2410
Не получается решить два уравнения.
Приложения:
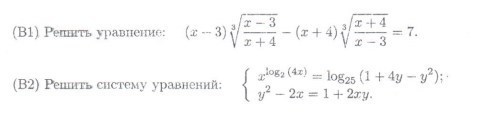
Ответы
Автор ответа:
0
1) ![(x-3) sqrt[3]{ frac{x-3}{x+4} } -(x+4) sqrt[3]{ frac{x+4}{x-3} } =7 (x-3) sqrt[3]{ frac{x-3}{x+4} } -(x+4) sqrt[3]{ frac{x+4}{x-3} } =7](https://tex.z-dn.net/?f=%28x-3%29+sqrt%5B3%5D%7B+frac%7Bx-3%7D%7Bx%2B4%7D+%7D+-%28x%2B4%29+sqrt%5B3%5D%7B+frac%7Bx%2B4%7D%7Bx-3%7D+%7D+%3D7)
![sqrt[3]{ frac{x-3}{x+4} } = sqrt[3]{ frac{x+4-7}{x+4} }= sqrt[3]{1- frac{7}{x+4} } textless 1 sqrt[3]{ frac{x-3}{x+4} } = sqrt[3]{ frac{x+4-7}{x+4} }= sqrt[3]{1- frac{7}{x+4} } textless 1](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B+frac%7Bx-3%7D%7Bx%2B4%7D+%7D+%3D+sqrt%5B3%5D%7B+frac%7Bx%2B4-7%7D%7Bx%2B4%7D+%7D%3D+sqrt%5B3%5D%7B1-+frac%7B7%7D%7Bx%2B4%7D+%7D++textless++1+)
Обозначим этот корень как 1-a.
Тогда![sqrt[3]{ frac{x+4}{x-3} } textgreater 1 sqrt[3]{ frac{x+4}{x-3} } textgreater 1](https://tex.z-dn.net/?f=sqrt%5B3%5D%7B+frac%7Bx%2B4%7D%7Bx-3%7D+%7D+textgreater++1) , обозначим его 1+b
, обозначим его 1+b
Получаем
(x-3)(1-a) - (x+4)(1+b) = x-3-a(x-3)-x-4-b(x+4) = -7-a(x-3)-b(x+4)<0,
потому что а и b > 0
Это уравнение решений не имеет.
2)
По определению логарифма
x > 0
-y^2+4y+1>0, то есть y ∈ (2-√5; 2+√5)
Вершина параболы y = 2, при этом 1+4y-y^2=5

Из 2 уравнения при y = 2 получается
4 - 2x = 1 + 4x
3 = 6x
x = 1/2
Подставляем в 1 уравнение

Совпало
Ответ: x = 1/2; y = 2
Обозначим этот корень как 1-a.
Тогда
Получаем
(x-3)(1-a) - (x+4)(1+b) = x-3-a(x-3)-x-4-b(x+4) = -7-a(x-3)-b(x+4)<0,
потому что а и b > 0
Это уравнение решений не имеет.
2)
По определению логарифма
x > 0
-y^2+4y+1>0, то есть y ∈ (2-√5; 2+√5)
Вершина параболы y = 2, при этом 1+4y-y^2=5
Из 2 уравнения при y = 2 получается
4 - 2x = 1 + 4x
3 = 6x
x = 1/2
Подставляем в 1 уравнение
Совпало
Ответ: x = 1/2; y = 2
Автор ответа:
0
еще как имеет. -0,5 подставь в исходное => 7=7
Похожие вопросы
Предмет: Математика,
автор: elapla
Предмет: Химия,
автор: Аноним
Предмет: Алгебра,
автор: Infernofb
Предмет: Биология,
автор: mel173