Предмет: Математика,
автор: nakuruma
меня интересует ход решения, так как не совсем могу понять что из чего вышло. Если кто может - объясните русским языком. Нижняя строка решения мне не понятна совсем. что от куда взялось?
* В партии из N изделий n изделий имеют скрытый дефект. Какова вероятность
того, что из взятых наугад m изделий k изделий являются дефектными.
N = 20, n = 5, m = 4, k = 2.
Приложения:
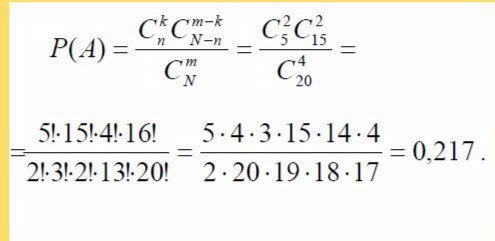
Ответы
Автор ответа:
0
верхняя строка - это основные формулы комбинаторики,
С²₅ = 5!/(5-2)!*2! = 5!/3!*2! - в числителе факториал (обозначается !) нижнего индекса (здесь равен 5), в знаменателе факториал разности нижнего и верхнего индексов (5-2) умножить на факториал верхнего индекса
Таким же образом распишем
С²₁₅ = 15!/(15-2)!*2! = 15!/13!*2!
С⁴₂₀ = 20!/(20-4)!*4! = 20!/16!*4!
а теперь заменим
С²₅ * С²₁₅ = 5!/(3!*2!) * 15!/ (13!*2!) = (5!*15!)/(3!*2!*13!*2!)
а теперь всю дробь заменим
(С²₅ * С²₁₅ )/С⁴₂₀ = (С²₅ * С²₁₅ ) * 1/С⁴₂₀ =
=(5!*15!)/(3!*2!*13!*2!) * (16!*4!)/20! =
= (5!*15! *16!*4!)/(3!*2!*13!*2!*20!)
а дальше факториал представляете в виде произведения и сокращаете одинаковые множители
С²₅ = 5!/(5-2)!*2! = 5!/3!*2! - в числителе факториал (обозначается !) нижнего индекса (здесь равен 5), в знаменателе факториал разности нижнего и верхнего индексов (5-2) умножить на факториал верхнего индекса
Таким же образом распишем
С²₁₅ = 15!/(15-2)!*2! = 15!/13!*2!
С⁴₂₀ = 20!/(20-4)!*4! = 20!/16!*4!
а теперь заменим
С²₅ * С²₁₅ = 5!/(3!*2!) * 15!/ (13!*2!) = (5!*15!)/(3!*2!*13!*2!)
а теперь всю дробь заменим
(С²₅ * С²₁₅ )/С⁴₂₀ = (С²₅ * С²₁₅ ) * 1/С⁴₂₀ =
=(5!*15!)/(3!*2!*13!*2!) * (16!*4!)/20! =
= (5!*15! *16!*4!)/(3!*2!*13!*2!*20!)
а дальше факториал представляете в виде произведения и сокращаете одинаковые множители
Приложения:

Автор ответа:
0
не знаю. добавьте, пожалуйста
Автор ответа:
0
ок! добавлю фото. рукой быстрее писать
Автор ответа:
0
жду
Автор ответа:
0
если нет вопросов - иду спать
Автор ответа:
0
спасибо огромнейшее
Автор ответа:
0
по формуле классической вероятности:
Пусть w - кол-во всех возможных исходов
 - кол-во благоприятных исходов.
- кол-во благоприятных исходов.
Тогда вероятность наступления события A:

Посчитаем w:
Мы берём m изделий из N штук, итого
Посчитаем :
:
для начала выберем всеми способами k изделий из всех что есть с дефектом(у нас n).
Итого мы взяли k≤m изделий. И если k≠m, то нам нужно добрать m-k изделий без дефекта(их у нас N-n). .
.
Перемножаем сочетания и получаем:

Посчитаем нашу вероятность(формула для сочетаний: ):
):
![P(A)=frac{v_a}{w}=frac{C_N^k*C^{m-k}_{N-n}}{C_N^m}=frac{C_5^2C_{15}^2}{C_{20}^4}=frac{frac{5!}{2!(5-2)!}*frac{15!}{2!(15-2)!}}{frac{20!}{4!(20-4)!}}=\=frac{5!*15!*4!*(20-4)!}{2!(5-2)!*2!(15-2)!*20!}=frac{5!*15!*4!*16!}{2!*3!*2!*13!*20!}=\=[20!=16!*17*18*19*20]=\=frac{(3!*4*5)*(13!*14*15)*(1*2*3*4)*16!}{2*3!*2*13!*16!*17*18*19*20}=frac{4*5*14*15*2*3*4}{2*2*17*18*19*20}=0.217 P(A)=frac{v_a}{w}=frac{C_N^k*C^{m-k}_{N-n}}{C_N^m}=frac{C_5^2C_{15}^2}{C_{20}^4}=frac{frac{5!}{2!(5-2)!}*frac{15!}{2!(15-2)!}}{frac{20!}{4!(20-4)!}}=\=frac{5!*15!*4!*(20-4)!}{2!(5-2)!*2!(15-2)!*20!}=frac{5!*15!*4!*16!}{2!*3!*2!*13!*20!}=\=[20!=16!*17*18*19*20]=\=frac{(3!*4*5)*(13!*14*15)*(1*2*3*4)*16!}{2*3!*2*13!*16!*17*18*19*20}=frac{4*5*14*15*2*3*4}{2*2*17*18*19*20}=0.217](https://tex.z-dn.net/?f=P%28A%29%3Dfrac%7Bv_a%7D%7Bw%7D%3Dfrac%7BC_N%5Ek%2AC%5E%7Bm-k%7D_%7BN-n%7D%7D%7BC_N%5Em%7D%3Dfrac%7BC_5%5E2C_%7B15%7D%5E2%7D%7BC_%7B20%7D%5E4%7D%3Dfrac%7Bfrac%7B5%21%7D%7B2%21%285-2%29%21%7D%2Afrac%7B15%21%7D%7B2%21%2815-2%29%21%7D%7D%7Bfrac%7B20%21%7D%7B4%21%2820-4%29%21%7D%7D%3D%5C%3Dfrac%7B5%21%2A15%21%2A4%21%2A%2820-4%29%21%7D%7B2%21%285-2%29%21%2A2%21%2815-2%29%21%2A20%21%7D%3Dfrac%7B5%21%2A15%21%2A4%21%2A16%21%7D%7B2%21%2A3%21%2A2%21%2A13%21%2A20%21%7D%3D%5C%3D%5B20%21%3D16%21%2A17%2A18%2A19%2A20%5D%3D%5C%3Dfrac%7B%283%21%2A4%2A5%29%2A%2813%21%2A14%2A15%29%2A%281%2A2%2A3%2A4%29%2A16%21%7D%7B2%2A3%21%2A2%2A13%21%2A16%21%2A17%2A18%2A19%2A20%7D%3Dfrac%7B4%2A5%2A14%2A15%2A2%2A3%2A4%7D%7B2%2A2%2A17%2A18%2A19%2A20%7D%3D0.217)
Пусть w - кол-во всех возможных исходов
Тогда вероятность наступления события A:
Посчитаем w:
Мы берём m изделий из N штук, итого
Посчитаем
для начала выберем всеми способами k изделий из всех что есть с дефектом(у нас n).
Итого мы взяли k≤m изделий. И если k≠m, то нам нужно добрать m-k изделий без дефекта(их у нас N-n).
Перемножаем сочетания и получаем:
Посчитаем нашу вероятность(формула для сочетаний:
Приложения:

Автор ответа:
0
спасибо большущее!!!
Похожие вопросы
Предмет: Французский язык,
автор: VSEMENTSOVA
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: thepolli50
Предмет: Геометрия,
автор: miumiumiu2015
Предмет: Биология,
автор: medkova