Предмет: Геометрия,
автор: kingpie
В окружность,диаметром 10 корней 2,вписан шестиугольник,у которого одна сторона =10,а все остальные равны между собой.Найдите углы этого шестиугольника
Ответы
Автор ответа:
0
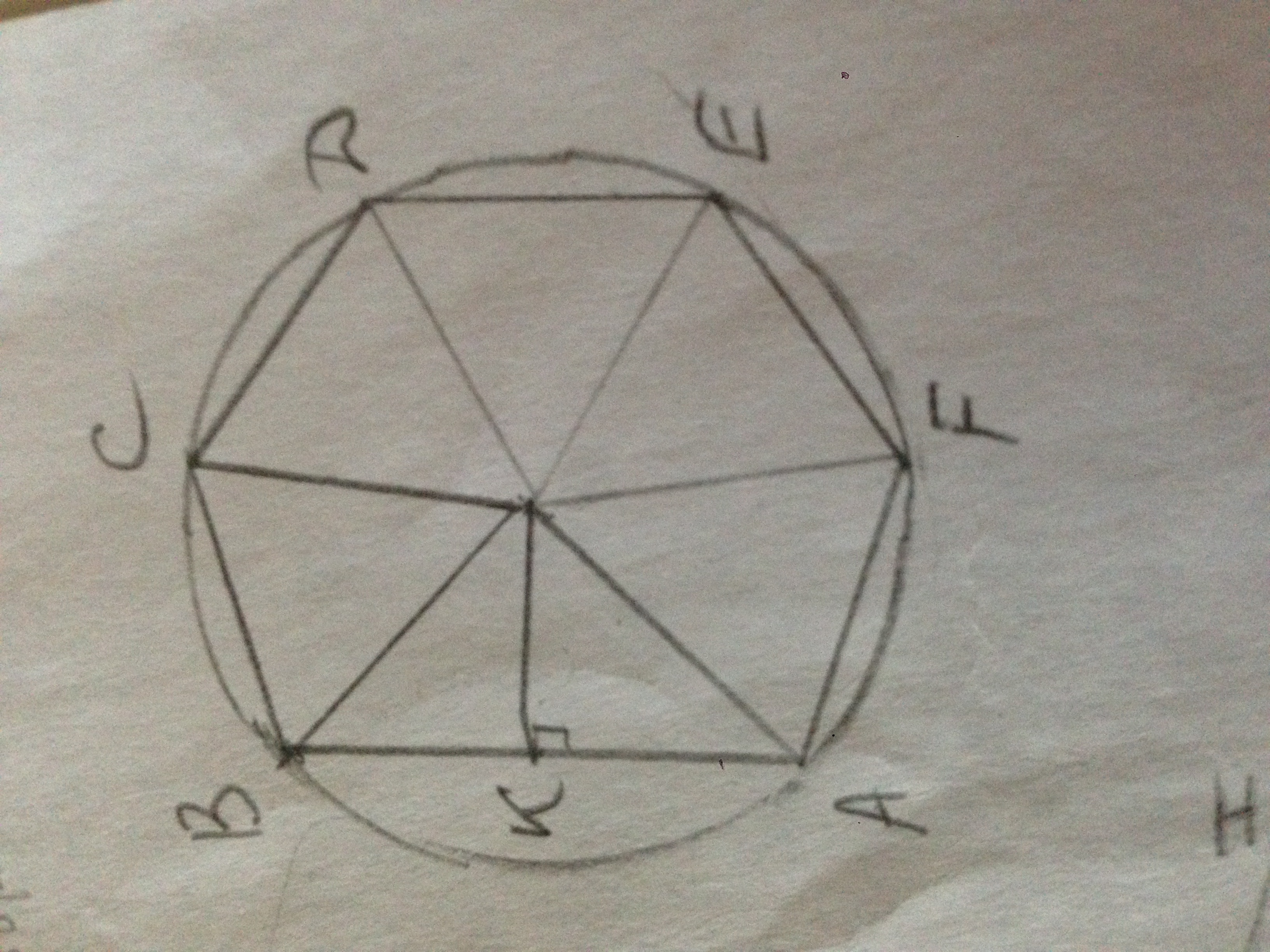
АВСДЕФ - шестиугольник, АВ=10, ВС=СД=ДЕ=ЕФ=АФ.
В тр-ке ВОК=ВО=D/2=5√2, ВК=ВК/2=5, sin(ВОК)=ВК/ВО=5/5√2=√2/2.
∠ВОК=45°, ∠АОВ=90°.
∠ОАВ=∠ОВА=45°.
В оставшейся части окружности расположено пять равных тр-ков, градусная мера центрального угла каждого из них равна: ∠ВОС=(360-90)/5=54°. ∠ОВС=(180-54)/2=63°.
Градусная мера угла шестиугольника, образованного двумя равными треугольниками, равна сумме углов при основании одного из них.
∠ВСД=63+63=126°.
В шестиугольнике ∠С=∠Д=∠Е=∠Ф=126° - это ответ.
∠А=∠В=∠ОВА+∠ОВС=45+63=108° - это ответ.
В тр-ке ВОК=ВО=D/2=5√2, ВК=ВК/2=5, sin(ВОК)=ВК/ВО=5/5√2=√2/2.
∠ВОК=45°, ∠АОВ=90°.
∠ОАВ=∠ОВА=45°.
В оставшейся части окружности расположено пять равных тр-ков, градусная мера центрального угла каждого из них равна: ∠ВОС=(360-90)/5=54°. ∠ОВС=(180-54)/2=63°.
Градусная мера угла шестиугольника, образованного двумя равными треугольниками, равна сумме углов при основании одного из них.
∠ВСД=63+63=126°.
В шестиугольнике ∠С=∠Д=∠Е=∠Ф=126° - это ответ.
∠А=∠В=∠ОВА+∠ОВС=45+63=108° - это ответ.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Contur44
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: katyasakalova1932
Предмет: Математика,
автор: mvideonsk
Предмет: Биология,
автор: natali1977731