Предмет: Математика,
автор: 34wrfcd
Помогите пожалуйста решить 1 и 2 задания.
Приложения:
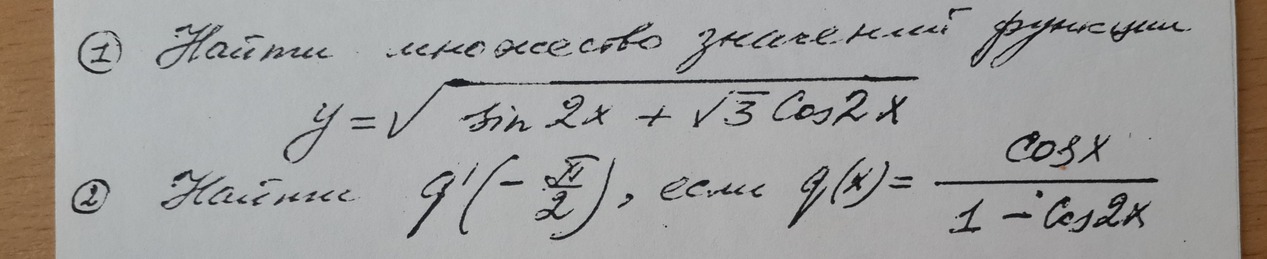
Ответы
Автор ответа:
0
В первом задании нужно подкоренное выражение преобразовать в косинус суммы или в синус суммы, для этого выносим за скобку число 2. Это корень квадратный из суммы квадратов коэффициентов при синусе и косинусе.
2(1/2 * sin2x+√3/2 * cos2x) = 2*(cos π/3 * sin2x + sinπ/3 * cos2x) =
=2*(sin(2x+π/3)). Теперь мы видим, что подкоренное значение принимает значения из интервала [-2;2]. Но отрицательные значения для подкоренного выражения недопустимы, остается множество [0;2].
А значит у∈[0;√2].
2(1/2 * sin2x+√3/2 * cos2x) = 2*(cos π/3 * sin2x + sinπ/3 * cos2x) =
=2*(sin(2x+π/3)). Теперь мы видим, что подкоренное значение принимает значения из интервала [-2;2]. Но отрицательные значения для подкоренного выражения недопустимы, остается множество [0;2].
А значит у∈[0;√2].
Автор ответа:
0
смотри решение на фото.
Приложения:

Похожие вопросы
Предмет: Окружающий мир,
автор: andrejponosov705
Предмет: Математика,
автор: ChitaBogis
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: Freakazoid