Предмет: Алгебра,
автор: Прелесть98
Исследуйте функцию и постройте ее график:
f(x)=x^5+20x^2+3
на промежутке [-1;1]
Ответы
Автор ответа:
0
Алгоритм такой:
1) Найдём производную:

2. Найдём экстремумы:

Заданной области принадлежит точка .
.
3. Найдём область убываения и возрастания относительно нуля: с помощью метода интервалов установим, функция убывает на промежутке![[-1;0] [-1;0]](https://tex.z-dn.net/?f=%5B-1%3B0%5D) и растёт — на промежутке
и растёт — на промежутке ![[0;1] [0;1]](https://tex.z-dn.net/?f=%5B0%3B1%5D)
4. Найдём вторую производную и исследуем функцию на выпуклость:
![f''(x)=(5x^4+40x)'=20x^3+40.\\20x^3+40=0\x^3+2=0\x^3=-2\x= sqrt[3]{-2} f''(x)=(5x^4+40x)'=20x^3+40.\\20x^3+40=0\x^3+2=0\x^3=-2\x= sqrt[3]{-2}](https://tex.z-dn.net/?f=f%27%27%28x%29%3D%285x%5E4%2B40x%29%27%3D20x%5E3%2B40.%5C%5C20x%5E3%2B40%3D0%5Cx%5E3%2B2%3D0%5Cx%5E3%3D-2%5Cx%3D+sqrt%5B3%5D%7B-2%7D+)
Нам повезло — экстремум второй производной лежит вне нашей области. Методом интервалов установим, что функция на области![[-1;1] [-1;1]](https://tex.z-dn.net/?f=%5B-1%3B1%5D) является вогнутой.
является вогнутой.
5. Теперь можно строить график. Найдём значение функции в точках −1 и 1: и
и 
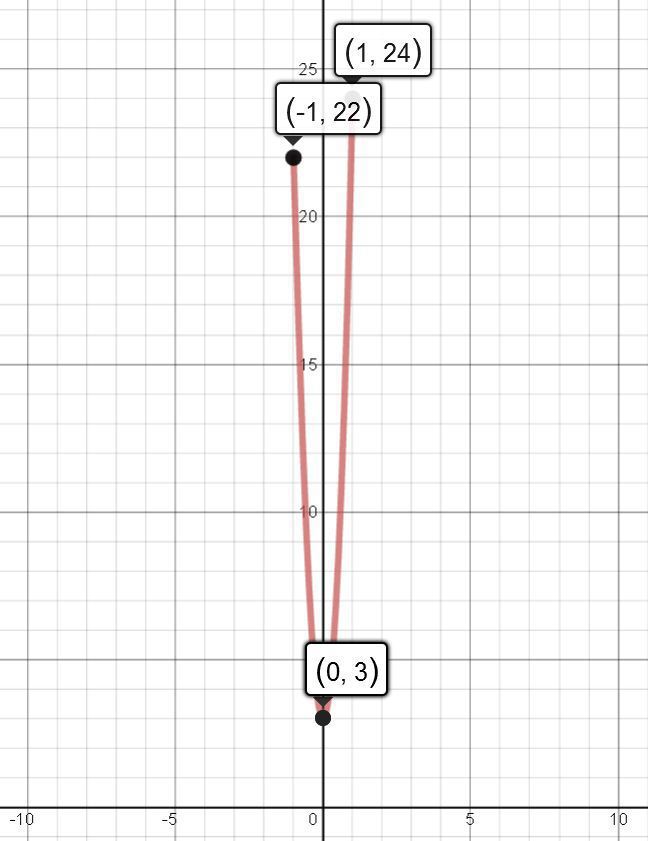
6. Суммируя все предыдущие пункты, наносим такие точки:

И теперь соединяем их так, чтобы функция убывала на [-1; 0] и росла— на [0; 1]. И не забываем, что функция везде должна быть вогнута.
Если правильно построишь, должно получиться так:
1) Найдём производную:
2. Найдём экстремумы:
Заданной области принадлежит точка
3. Найдём область убываения и возрастания относительно нуля: с помощью метода интервалов установим, функция убывает на промежутке
4. Найдём вторую производную и исследуем функцию на выпуклость:
Нам повезло — экстремум второй производной лежит вне нашей области. Методом интервалов установим, что функция на области
5. Теперь можно строить график. Найдём значение функции в точках −1 и 1:
6. Суммируя все предыдущие пункты, наносим такие точки:
И теперь соединяем их так, чтобы функция убывала на [-1; 0] и росла— на [0; 1]. И не забываем, что функция везде должна быть вогнута.
Если правильно построишь, должно получиться так:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: sagynysh0929
Предмет: Математика,
автор: dyexfnf
Предмет: Музыка,
автор: derghj24
Предмет: История,
автор: Sofia032002