Question

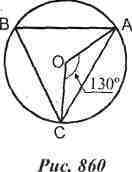
Угол АОС=130, АВ : BC = 11 : 12. Найти: BCA, BAC.

Answer 1

Вершины вписанного треугольника АВС разделили окружность на три дуги. 

Вся окружность содержит 360º

Дуга АС =центральному углу АОС=130º

На две другие дуги приходится

◡АВ+◡ВС=360º-130º=230º

Из отношения данных дуг находим сумму частей, содержащихся в них:

11+12=23 

230º:23=10º в одной части. 

◡АВ=10º*11=110º , и тогда вписанный угол ВСА, который опирается на неё, равен её половине ( по свойству вписанного угла):

∠ВСА=110º:2=55º

◡ВС=10º*12=120º

и вписанный угол ВАС равен половине дуги ВС:

∠ВАС=120º:2=60º

Ну, и третий угол равен половине центрального угла:

∠АВС=∠АОС:2=65º