Предмет: Алгебра,
автор: nKrynka
Помогите, пожалуйста, решить задачу:
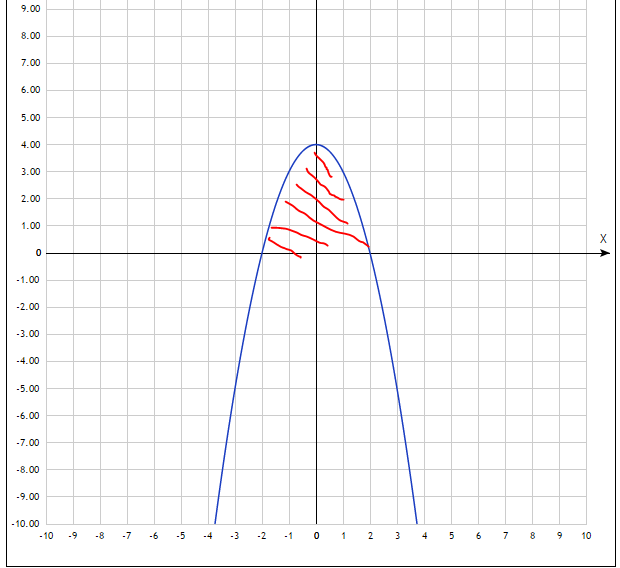
Найти площадь фигуры, ограниченной линиями
y = 4 - x^2, y = 0, x = - 1, x = 1
С рисунком, пожалуйста.
Ответы
Автор ответа:
0
Площадь рана интегралу от функции (4-х²) в пределах от 1 до -1
S=4x-x³/3|1-(-1)=4-1/3+4-1/3=8-2/3=7 1/3
S=4x-x³/3|1-(-1)=4-1/3+4-1/3=8-2/3=7 1/3
Приложения:
Автор ответа:
0
Человек попросил с рисунком... Я не понимаю, вы специально торопитесь, что бы обогнать?
Автор ответа:
0
Спасибо!
Автор ответа:
0
Даны границы фигуры:
![[-1,1] [-1,1]](https://tex.z-dn.net/?f=%5B-1%2C1%5D) - отрезок
- отрезок
Часть графика на данном отрезке находиться над осью иксов. Следовательно, интеграл положительный.
на данном отрезке находиться над осью иксов. Следовательно, интеграл положительный.
Теперь составим интеграл:


Часть графика
Теперь составим интеграл:
Приложения:
Автор ответа:
0
На графике должны быть прямые: x = - 1 и x = 1. Площадь находится между ними?
Автор ответа:
0
Да, я случайно отметил всю фигуру на осью икс...
Похожие вопросы
Предмет: Математика,
автор: alexander553
Предмет: Алгебра,
автор: nurbekasylbek
Предмет: Русский язык,
автор: marat05101974
Предмет: Математика,
автор: Misiss5katya